|
by Lawrence H. Ford and Thomas A. Roman Scientific American, January 2000 from TerryBoyce Website recovered through WayBackMachine Website
Can a region of space contain less than nothing?
Common sense would say no; the most one could do is remove all matter and radiation and be left with vacuum. But quantum physics has a proven ability to confound intuition, and this case is no exception. A region of space, it turns out, can contain less than nothing. Its energy per unit volume - the energy density - can be less than zero.
Needless to say, the implications are bizarre. According to Einstein’s theory of gravity, general relativity, the presence of matter and energy warps the geometric fabric of space and time. What we perceive as gravity is the space-time distortion produced by normal, positive energy or mass.
But when negative energy or mass - so-called exotic matter - bends space-time, all sorts of amazing phenomena might become possible: traversable wormholes, which could act as tunnels to otherwise distant parts of the universe; warp drive, which would allow for faster-than-light travel; and time machines, which might permit journeys into the past.
Negative energy could even be used to make perpetual-motion machines or to destroy black holes. A Star Trek episode could not ask for more.
For physicists, these ramifications set off alarm bells. The potential paradoxes of backward time travel–such as killing your grandfather before your father is conceived–have long been explored in science fiction, and the other consequences of exotic matter are also problematic.
They raise a question of fundamental importance: Do the laws of physics that permit negative energy place any limits on its behavior?
We and others have discovered that nature imposes stringent constraints on the magnitude and duration of negative energy, which (unfortunately, some would say) appear to render the construction of wormholes and warp drives very unlikely.
Double Negative
Before proceeding further, we should draw the reader’s attention to what negative energy is not.
It should not be confused with antimatter, which has positive energy. When an electron and its antiparticle, a positron, collide, they annihilate. The end products are gamma rays, which carry positive energy. If antiparticles were composed of negative energy, such an interaction would result in a final energy of zero.
One should also not confuse negative energy with the energy associated with the cosmological constant, postulated in inflationary models of the universe [see "Cosmological Antigravity," by Lawrence M. Krauss; SCIENTIFIC AMERICAN, January 1999]. Such a constant represents negative pressure but positive energy. (Some authors call this exotic matter; we reserve the term for negative energy densities.)
The concept of negative energy is not pure fantasy; some of its effects have even been produced in the laboratory. They arise from Heisenberg’s uncertainty principle, which requires that the energy density of any electric, magnetic or other field fluctuate randomly. Even when the energy density is zero on average, as in a vacuum, it fluctuates.
Thus, the quantum vacuum can never remain empty in the classical sense of the term; it is a roiling sea of "virtual" particles spontaneously popping in and out of existence [see "Exploiting Zero-Point Energy," by Philip Yam; SCIENTIFIC AMERICAN, December 1997]. In quantum theory, the usual notion of zero energy corresponds to the vacuum with all these fluctuations.
So if one can somehow contrive to dampen the undulations, the vacuum will have less energy than it normally does–that is, less than zero energy.
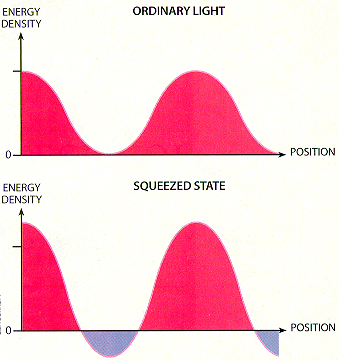
As an example, researchers in quantum optics have created special states of fields in which destructive quantum interference suppresses the vacuum fluctuations. These so-called squeezed vacuum states involve negative energy. More precisely, they are associated with regions of alternating positive and negative energy.
The total energy averaged over all space remains positive; squeezing the vacuum creates negative energy in one place at the price of extra positive energy elsewhere. A typical experiment involves laser beams passing through nonlinear optical materials [see "Squeezed Light," by Richart E. Slusher and Bernard Yurke; SCIENTIFIC AMERICAN, May 1988]. The intense laser light induces the material to create pairs of light quanta, photons. These photons alternately enhance and suppress the vacuum fluctuations, leading to regions of positive and negative energy, respectively.
Another method for producing negative energy introduces geometric boundaries into a space. In 1948 Dutch physicist Hendrik B. G. Casimir showed that two uncharged parallel metal plates alter the vacuum fluctuations in such a way as to attract each other. The energy density between the plates was later calculated to be negative. In effect, the plates reduce the fluctuations in the gap between them; this creates negative energy and pressure, which pulls the plates together.
The narrower the gap, the more negative the energy and pressure, and the stronger is the attractive force.
The Casimir effect has recently been measured by Steve K. Lamoreaux of Los Alamos National Laboratory and by Umar Mohideen of the University of California at Riverside and his colleague Anushree Roy. Similarly, in the 1970s Paul C. W. Davies and Stephen A. Fulling, then at King’s College at the University of London, predicted that a moving boundary, such as a moving mirror, could produce a flux of negative energy.
For both the Casimir effect and squeezed states, researchers have measured only the indirect effects of negative energy.
Direct detection is more difficult but might be possible using atomic spins, as Peter G. Grove, then at the British Home Office, Adrian C. Ottewill, then at the University of Oxford, and one of us (Ford) suggested in 1992.
Gravity and Levity
The concept of negative energy arises in several areas of modern physics.
It has an intimate link with black holes, those mysterious objects whose gravitational field is so strong that nothing can escape from within their boundary, the event horizon.
In 1974 Stephen W. Hawking of the University of Cambridge made his famous prediction that black holes evaporate by emitting radiation [see "The Quantum Mechanics of Black Holes," by Stephen W. Hawking; SCIENTIFIC AMERICAN, January 1977].
A black hole radiates energy at a rate inversely proportional to the square of its mass. Although the evaporation rate is large only for subatomic size black holes, it provides a crucial link between the laws of black holes and the laws of thermodynamics. The Hawking radiation allows black holes to come into thermal equilibrium with their environment.
At first glance, evaporation leads to a contradiction. The horizon is a one-way street; energy can only flow inward. So how can a black hole radiate energy outward? Because energy must be conserved, the production of positive energy - which distant observers see as the Hawking radiation - is accompanied by a flow of negative energy into the hole. Here the negative energy is produced by the extreme space-time curvature near the hole, which disturbs the vacuum fluctuations. In this way, negative energy is required for the consistency of the unification of black hole physics with thermodynamics.
The black hole is not the only curved region of space-time where negative energy seems to play a role. Another is the worm hole - a hypothesized type of tunnel that connects one region of space and time to another. Physicists used to think that wormholes exist only on the very finest length scales, bubbling in and out of existence like virtual particles [see "Quantum Gravity, by Bryce S. DeWitt; SCIENTIFIC AMERICAN, December 1983].
In the early 1960s physicists Robert Fuller and John A. Wheeler showed that larger wormholes would collapse under their own gravity so rapidly that even a beam of light would not have enough time to travel through them.
But in the late 1980s various researchers - notably Michael S. Morris and Kip S. Thorne of the California Institute of Technology and Matt Visser of Washington University - found otherwise.
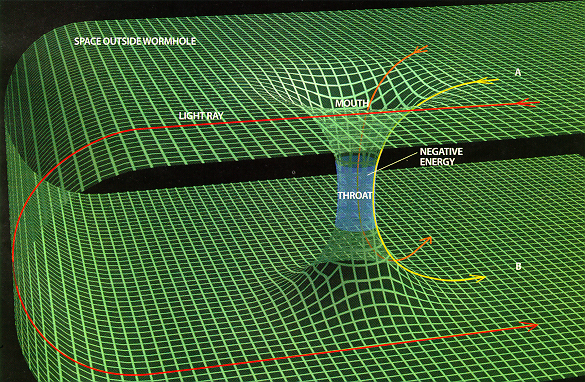
Certain wormholes could in fact be made large enough for a person or spaceship. Someone might enter the mouth of a wormhole stationed on Earth, walk a short distance inside the wormhole and exit the other mouth in, say, the Andromeda galaxy. The catch is that traversable wormholes require negative energy. Because negative energy is gravitationally repulsive, it would prevent the wormhole from collapsing.
For a wormhole to be traversable, it ought to (at bare minimum) allow signals, in the form of light rays, to pass through it. Light rays entering one mouth of a wormhole are converging, but to emerge from the other mouth, they must defocus - in other words, they must go from converging to diverging somewhere in between [see illustration below]. This defocusing requires negative energy.
Whereas the curvature of space produced by the attractive gravitational field of ordinary matter acts like a converging lens, negative energy acts like a diverging lens.
No Dilithium Needed
Such space-time contortions would enable another staple of science fiction as well: faster-than-light travel.
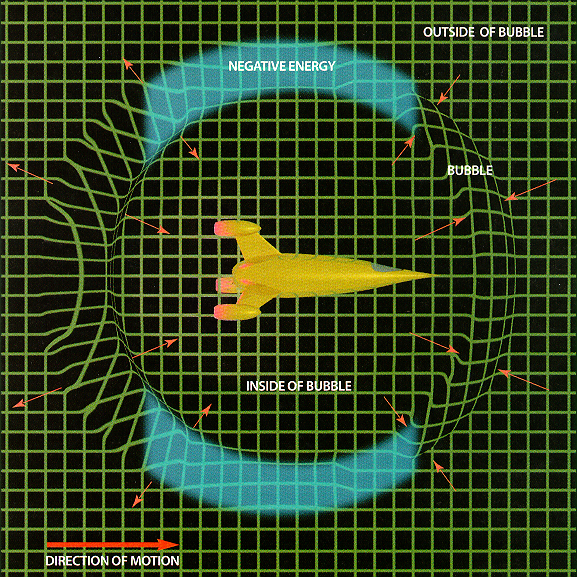
In 1994 Miguel Alcubierre Moya, then at the University of Wales at Cardiff, discovered a solution to Einstein’s equations that has many of the desired features of warp drive. It describes a space-time bubble that transports a starship at arbitrarily high speeds relative to observers outside the bubble. Calculations show that negative energy is required.
Warp drive might appear to violate Einstein’s special theory of relativity. But special relativity says that you cannot outrun a light signal in a fair race in which you and the signal follow the same route. When space-time is warped, it might be possible to beat a light signal by taking a different route, a shortcut.
The contraction of space-time in front of the bubble and the expansion behind it create such a shortcut [see illustration below].
One problem with Alcubierre’s original model, pointed out by Sergei V. Krasnikov of the Central Astronomical Observatory at Pulkovo near St. Petersburg, is that the interior of the warp bubble is causally disconnected from its forward edge.
A starship captain on the inside cannot steer the bubble or turn it on or off; some external agency must set it up ahead of time. To get around this problem, Krasnikov proposed a "superluminal subway," a tube of modified space-time (not the same as a wormhole) connecting Earth and a distant star.
Within the tube, superluminal travel in one direction is possible. During the outbound journey at sublight speed, a spaceship crew would create such a tube. On the return journey, they could travel through it at warp speed. Like warp bubbles, the subway involves negative energy. It has since been shown by Ken D. Olum of Tufts University and by Visser, together with Bruce Bassett of Oxford and Stefano Liberati of the International School for Advanced Studies in Trieste, that any scheme for faster-than-light travel requires the use of negative energy.
If one can construct wormholes or warp drives, time travel might become possible. The passage of time is relative; it depends on the observer’s velocity. A person who leaves Earth in a spaceship, travels at near lightspeed and returns will have aged less than someone who remains on Earth.
If the traveler manages to outrun a light ray, perhaps by taking a shortcut through a wormhole or a warp bubble, he may return before he left. Morris, Thorne and Ulvi Yurtsever, then at Caltech, proposed a wormhole time machine in 1988, and their paper has stimulated much research on time travel over the past decade.
In 1992 Hawking proved that any construction of a time machine in a finite region of space-time inherently requires negative energy.
Negative energy is so strange that one might think it must violate some law of physics.
Before and after the creation of equal amounts of negative and positive energy in previously empty space, the total energy is zero, so the law of conservation of energy is obeyed. But there are many phenomena that conserve energy yet never occur in the real world. A broken glass does not reassemble itself, and heat does not spontaneously flow from a colder to a hotter body. Such effects are forbidden by the second law of thermodynamics.
This general principle states that the degree of disorder of a system–its entropy–cannot decrease on its own without an input of energy. Thus, a refrigerator, which pumps heat from its cold interior to the warmer outside room, requires an external power source. Similarly, the second law also forbids the complete conversion of heat into work.
Negative energy potentially conflicts with the second law. Imagine an exotic laser, which creates a steady outgoing beam of negative energy. Conservation of energy requires that a byproduct be a steady stream of positive energy. One could direct the negative energy beam off to some distant corner of the universe, while employing the positive energy to perform useful work.
This seemingly inexhaustible energy supply could be used to make a perpetual-motion machine and thereby violate the second law. If the beam were directed at a glass of water, it could cool the water while using the extracted positive energy to power a small motor–providing a refrigerator with no need for external power. These problems arise not from the existence of negative energy per se but from the unrestricted separation of negative and positive energy.
Unfettered negative energy would also have profound consequences for black holes. When a black hole forms by the collapse of a dying star, general relativity predicts the formation of a singularity, a region where the gravitational field becomes infinitely strong. At this point, general relativity–and indeed all known laws of physics–are unable to say what happens next.
This inability is a profound failure of the current mathematical description of nature. So long as the singularity is hidden within an event horizon, however, the damage is limited. The description of nature everywhere outside of the horizon is unaffected.
For this reason, Roger Penrose of Oxford proposed the cosmic censorship hypothesis:
For special types of charged or rotating black holes - known as extreme black holes - even a small increase in charge or spin, or a decrease in mass, could in principle destroy the horizon and convert the hole into a naked singularity.
Attempts to charge up or spin up these black holes using ordinary matter seem to fail for a variety of reasons.
One might instead envision producing a decrease in mass by shining a beam of negative energy down the hole, without altering its charge or spin, thus subverting cosmic censorship. One might create such a beam, for example, using a moving mirror. In principle, it would require only a tiny amount of negative energy to produce a dramatic change in the state of an extreme black hole.
Therefore, this might be the scenario in which negative energy is the most likely to produce macroscopic effects.
Not Separate and Not Equal
Fortunately (or not, depending on your point of view), although quantum theory allows the existence of negative energy, it also appears to place strong restrictions - known as quantum inequalities - on its magnitude and duration. These inequalities were first suggested by Ford in 1978.
Over the past decade they have been proved and refined by us and others, including Eanna E. Flanagan of Cornell University, Michael J. Pfenning, then at Tufts, Christopher J. Fewster and Simon P. Eveson of the University of York, and Edward Teo of the National University of Singapore.
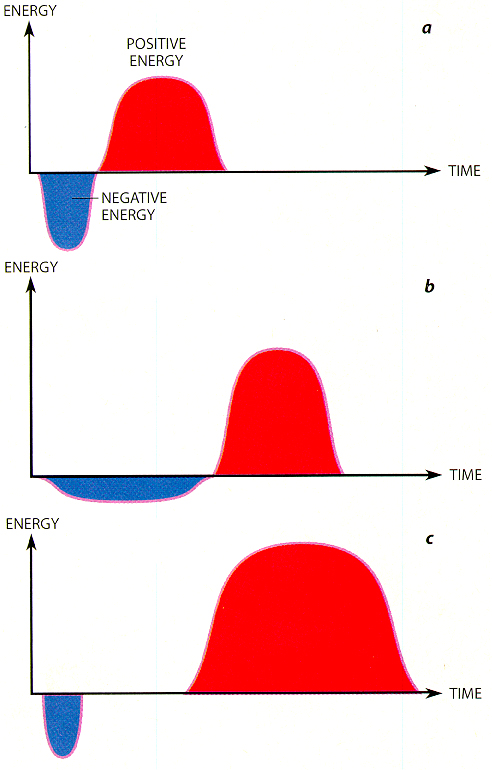
The inequalities bear some resemblance to the uncertainty principle. They say that a beam of negative energy cannot be arbitrarily intense for an arbitrarily long time. The permissible magnitude of the negative energy is inversely related to its temporal or spatial extent. An intense pulse of negative energy can last for a short time; a weak pulse can last longer. Furthermore, an initial negative energy pulse must be followed by a larger pulse of positive energy [see illustration below].
The larger the magnitude of the negative energy, the nearer must be its positive energy counterpart. These restrictions are independent of the details of how the negative energy is produced. One can think of negative energy as an energy loan. Just as a debt is negative money that has to be repaid, negative energy is an energy deficit.
As we will discuss below, the analogy goes even further.
In the Casimir effect, the negative energy density between the plates can persist indefinitely, but large negative energy densities require a very small plate separation.
The magnitude of the negative energy density is inversely proportional to the fourth power of the plate separation. Just as a pulse with a very negative energy density is limited in time, very negative Casimir energy density must be confined between closely spaced plates.
According to the quantum inequalities, the energy density in the gap can be made more negative than the Casimir value, but only temporarily. In effect, the more one tries to depress the energy density below the Casimir value, the shorter the time over which this situation can be maintained.
When applied to wormholes and warp drives, the quantum inequalities typically imply that such structures must either be limited to submicroscopic sizes, or if they are macroscopic the negative energy must be confined to incredibly thin bands. In 1996 we showed that a submicroscopic wormhole would have a throat radius of no more than about 10-32 meter.
This is only slightly larger than the Planck length, 10-35 meter, the smallest distance that has definite meaning. We found that it is possible to have models of wormholes of macroscopic size but only at the price of confining the negative energy to an extremely thin band around the throat. For example, in one model a throat radius of 1 meter requires the negative energy to be a band no thicker than 10-21 meter, a millionth the size of a proton.
Visser has estimated that the negative energy required for this size of wormhole has a magnitude equivalent to the total energy generated by 10 billion stars in one year. The situation does not improve much for larger wormholes. For the same model, the maximum allowed thickness of the negative energy band is proportional to the cube root of the throat radius. Even if the throat radius is increased to a size of one light-year, the negative energy must still be confined to a region smaller than a proton radius, and the total amount required increases linearly with the throat size.
It seems that wormhole engineers face daunting problems.
They must find a mechanism for confining large amounts of negative energy to extremely thin volumes. So-called cosmic strings, hypothesized in some cosmological theories, involve very large energy densities in long, narrow lines. But all known physically reasonable cosmic-string models have positive energy densities.
Warp drives are even more tightly constrained, as shown by Pfenning and Allen Everett of Tufts, working with us. In Alcubierre’s model, a warp bubble traveling at 10 times lightspeed (warp factor 2, in the parlance of Star Trek: The Next Generation) must have a wall thickness of no more than 10-32 meter.
A bubble large enough to enclose a starship 200 meters across would require a total amount of negative energy equal to 10 billion times the mass of the observable universe. Similar constraints apply to Krasnikov’s superluminal subway.
A modification of Alcubierre’s model was recently constructed by Chris Van Den Broeck of the Catholic University of Louvain in Belgium. It requires much less negative energy but places the starship in a curved space-time bottle whose neck is about 10-32 meter across, a difficult feat.
These results would seem to make it rather unlikely that one could construct wormholes and warp drives using negative energy generated by quantum effects.
Cosmic Flashing and Quantum Interest
The quantum inequalities prevent violations of the second law.
If one tries to use a pulse of negative energy to cool a hot object, it will be quickly followed by a larger pulse of positive energy, which reheats the object. A weak pulse of negative energy could remain separated from its positive counterpart for a longer time, but its effects would be indistinguishable from normal thermal fluctuations.
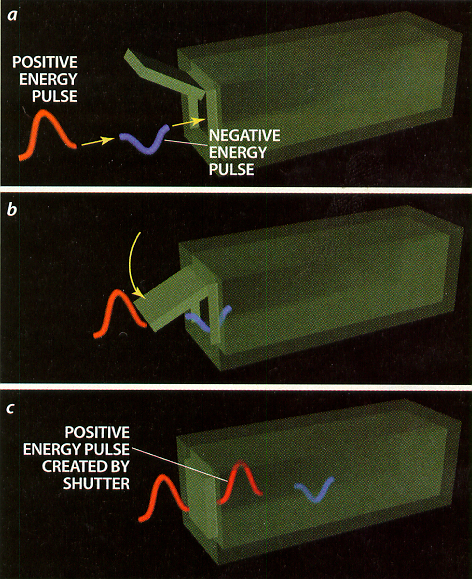
Attempts to capture or split off negative energy from positive energy also appear to fail. One might intercept an energy beam, say, by using a box with a shutter. By closing the shutter, one might hope to trap a pulse of negative energy before the offsetting positive energy arrives.
But the very act of closing the shutter creates an energy flux that cancels out the negative energy it was designed to trap [see illustration below].
We have shown that there are similar restrictions on violations of cosmic censorship.
A pulse of negative energy injected into a charged black hole might momentarily destroy the horizon, exposing the singularity within. But the pulse must be followed by a pulse of positive energy, which would convert the naked singularity back into a black hole - a scenario we have dubbed cosmic flashing. The best chance to observe cosmic flashing would be to maximize the time separation between the negative and positive energy, allowing the naked singularity to last as long as possible.
But then the magnitude of the negative energy pulse would have to be very small, according to the quantum inequalities. The change in the mass of the black hole caused by the negative energy pulse will get washed out by the normal quantum fluctuations in the hole’s mass, which are a natural consequence of the uncertainty principle. The view of the naked singularity would thus be blurred, so a distant observer could not unambiguously verify that cosmic censorship had been violated.
Recently we, and also Frans Pretorius, then at the University of Victoria, and Fewster and Teo, have shown that the quantum inequalities lead to even stronger bounds on negative energy. The positive pulse that necessarily follows an initial negative pulse must do more than compensate for the negative pulse; it must overcompensate.
The amount of overcompensation increases with the time interval between the pulses. Therefore, the negative and positive pulses can never be made to exactly cancel each other. The positive energy must always dominate–an effect known as quantum interest. If negative energy is thought of as an energy loan, the loan must be repaid with interest. The longer the loan period or the larger the loan amount, the greater is the interest. Furthermore, the larger the loan, the smaller is the maximum allowed loan period. Nature is a shrewd banker and always calls in its debts.
The concept of negative energy touches on many areas of physics: gravitation, quantum theory, thermodynamics. The interweaving of so many different parts of physics illustrates the tight logical structure of the laws of nature.
On the one hand, negative energy seems to be required to reconcile black holes with thermodynamics. On the other, quantum physics prevents unrestricted production of negative energy, which would violate the second law of thermodynamics. Whether these restrictions are also features of some deeper underlying theory, such as quantum gravity, remains to be seen.
Nature no doubt has more surprises in store.
The Authors
Lawrence H. Ford and Thomas A. Roman have collaborated on negative energy issues for over a decade. Ford received his Ph.D. from Princeton University in 1974, working under John Wheeler, one of the founders of black hole physics. He is now a professor of physics at Tufts University and works on problems in both general relativity and quantum theory, with a special interest in quantum fluctuations.
His other pursuits include hiking in the New England woods and gathering wild mushrooms. Roman received his Ph.D. in 1981 from Syracuse University under Peter Bergmann, who collaborated with Albert Einstein on unified field theory. Roman has been a frequent visitor at the Tufts Institute of Cosmology during the past 10 years and is currently a professor of physics at Central Connecticut State University.
His interests include the implications of negative energy for a quantum theory of gravity. He tends to avoid wild mushrooms.
Further Information xxx.lanl.gov/abs/gr-qc/9510071 on the World Wide Web. THE UNPHYSICAL NATURE OF WARP DRIVE. M. J. Pfenning and L. H. Ford in Classical and Quantum Gravity, Vol. 14, No. 7, pages 1743-1751; July 1997. Available at PARADOX LOST. Paul Davies in New Scientist, Vol. 157, No. 2126, page 26; March 21, 1998. TIME MACHINES: TIME TRAVEL IN PHYSICS, METAPHYSICS, AND SCIENCE FICTION. Paul J. Nahin. AIP Press, Springer-Verlag, 1999 second edition. THE QUANTUM INTEREST CONJECTURE. L. H. Ford and T. A. Roman in Physical Review D, Vol. 60, No. 10, Article No. 104018 (8 pages); November 15, 1999. Available at
|