|
from
Thunderbolts
Website
A diagram of the "electric Sun."
Illustration from Don
Scott's book, The Electric Sky.
The Sun rotates more rapidly at its equator than near its poles.
The magnetic fields near sunspots
reverse polarity from one eleven-year sunspot cycle to the next.
These and many other observed phenomena associated with the Sun give
strong indication that a high level of electrical activity is at
work on and above the surface of our local star.
Astronomers defend this standard model
by saying that all the processes they describe have been performed
in the laboratory and are well known. Nothing could be further from
the truth. Mankind has been doggedly struggling for over half a
century to create a sustained nuclear fusion reaction in the
laboratory. We have not even come close to doing it. It may not even
be possible.
Recently discovered inherent
instabilities in the plasma that is generated by the process may
make it impossible to control it and make it occur continuously.
Just to assume that such a sustained process is alive and well in
the Sun’s core is a stretch.
Rivers of plasma are electric currents.
Currents cause magnetic fields.
Eugene N. Parker correctly calls the coronal loops “bulges” in the Sun’s magnetic field.
He states:
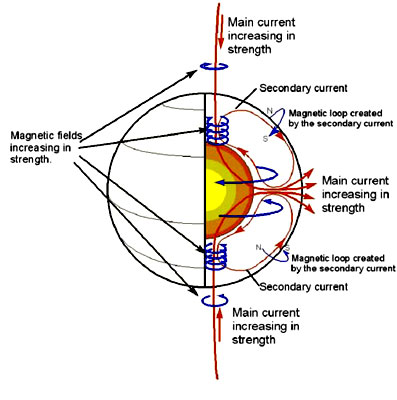
The image above shows a possible explanation of this phenomenon.
According to Alfvén’s stellar circuit, the main solar electric current flows into (or out of) each pole of the Sun. Making use of the “right-hand rule,” we can visualize the directions of the encircling magnetic fields created by that current. If the strength of this current is increasing, the magnetic field will strengthen as well.
Such time varying magnetic fields can induce secondary currents as shown in the figure.
The secondary current will only exist
when the magnitude of the linking magnetic field is growing or
shrinking. This effect is utilized here on Earth in AC transformers
and so is called transformer action.
The loop will move out above the Sun’s
surface and then return down into the surface forming a south
magnetic pole to the west of the current.
The resulting magnetic field will emerge (north magnetic pole) to the west of the current and return down to the surface (forming a south magnetic pole) to the east of the current.
Thus the action described by Parker (“The bipolar fields have opposite signs on opposite sides of the equator”) follows directly from Alfvén’s circuit. Of course, the locations of the subsurface currents shown in the image above are speculative at this point.
These reversing magnetic fields provide
a classic example of a phenomenon that cannot be understood without
reference to the electric currents that produce it.
Consequently the magnetic polarity of
the loops will also reverse. Notice that this mechanism does not
require the main solar driving current itself to reverse direction,
only to vary in amplitude. It also does not depend on the direction
of the primary current.
According to calculations by British scientists, the strength of the Sun’s magnetic field has doubled during the Twentieth Century alone. This finding may help to clarify the Sun’s contribution to climate change on Earth.
The hydrogen → helium fusion model does
not explain this phenomenon.
|