|
by Charlie Wood can be known through the behavior
of
just one of its countless particles. to understand what happens when black holes collide. In a surprise, they've shown that a single particle can describe a collision's entire gravitational wave...
Physicists have used Albert Einstein's theory of gravity to predict the rough contours of these gravitational waves as they pass through Earth, and wave after wave has been confirmed by the LIGO and Virgo gravitational-wave detectors.
But physicists are starting to flounder as they attempt to use Einstein's thorny equations to extract ultra-precise shapes of all possible reverberations.
These currently unknowable details
will be essential to fully understand the fine ripples that
next-generation observatories should pick up.
Several groups have recently made a surprising finding.
They have shown that the behavior of a gravitational (or electromagnetic) wave can be fully known through the actions of just one of its countless particles, as if we could learn the precise silhouette of a tsunami after examining a single water molecule.
a theoretical particle physicist at the Bhaumik Institute for Theoretical Physics
at the University of California, Los
Angeles.
The results could help future researchers interpret the sharper quivers in space-time that future observatories will record.
They also mark the next step in understanding how theories of quantum particles capture events taking place at our larger level of reality.
Quantum Cheat Codes
In principle, most physicists expect that quantum equations can also handle big objects.
We are, after all, largely clouds of electrons and quarks. In practice, however, Newton's laws suffice.
If we're calculating the arc of a cannonball, it doesn't make sense to start with an electron.
But gravitational wave astronomy is driving physicists to consider desperate measures.
When two black holes spiral toward each other and slam together, the shape of the resulting agitation of space-time depends on their masses, spins and other properties.
To fully understand the cosmic rumbles felt at gravitational wave facilities, physicists calculate ahead of time how various black hole pairings will jiggle space-time.
Einstein's equations of general relativity are too complicated to solve exactly, so some of LIGO/Virgo's waveforms came from precise supercomputer simulations.
Some of these might take a month.
The LIGO/Virgo collaboration relies on a collection of hundreds of thousands of waveforms, cobbled together from simulations and other quicker but rougher methods.
Particle physicists, at least in some cases, believe they can get faster and more accurate results.
From a zoomed-out perspective, black holes look a bit like massive particles, and physicists have spent decades thinking about what happens when particles go bump in the vacuum.
Alessandra Buonanno, a director of the Max Planck Institute
for Gravitational Physics.
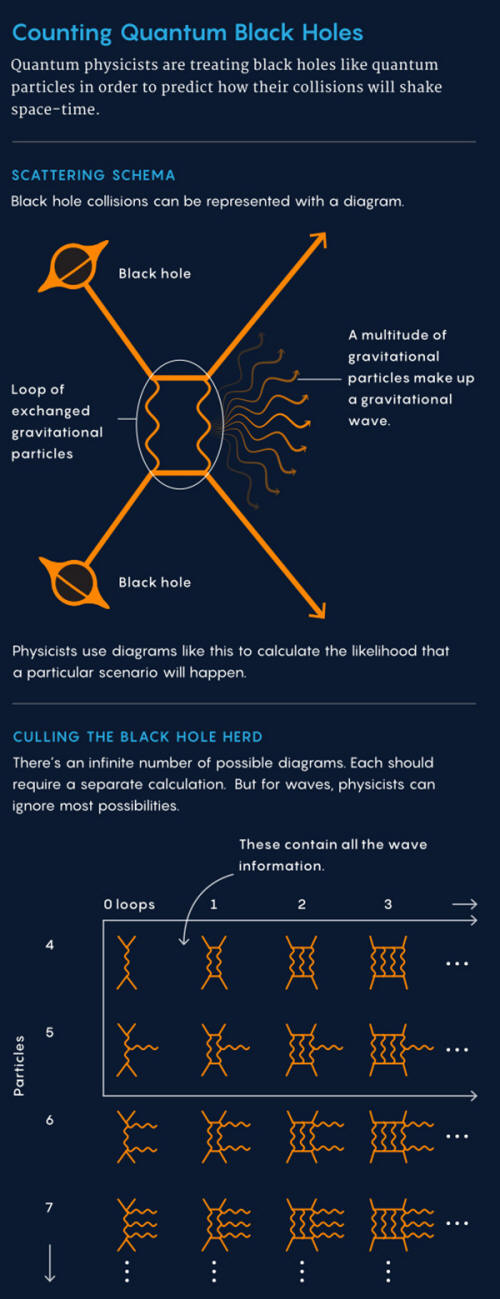
The main tools of the trade are known as amplitudes, mathematical expressions that give the odds of quantum events.
In recent years, Bern and other theorists applied four-point quantum amplitudes to the motion of colossal, classical black holes, matching - and in some cases exceeding - the precision of certain pieces of cutting-edge waveform calculations.
All in One
Classical physicists have steered clear of amplitudes for good reason.
Even a collision described by a four-point function - two particles in, two out - can temporarily generate any number of short-lived particles.
It gets worse.
But when two black holes come together, a four-point function isn't the only possibility.
Researchers must also consider the five-point function (a collision spitting out one particle of radiation), as well as the six-point function (a collision producing two particles) and so on.
A gravitational wave can be thought of as a collection of an infinite number of "graviton" particles, and an ideal calculation would cover them all - with an infinite number of functions, each with an infinite number of loops.
Merrill Sherman Quanta Magazine
In this quantum haystack of infinite width and depth, amplitude researchers need to identify the classical needles that would contribute to the shape of the wave.
One clue popped up in 2017, when Walter Goldberger of Yale University and Alexander Ridgway of the California Institute of Technology studied the classical radiation thrown off by two colliding objects with a sort of electric charge.
They took inspiration from a curious relationship between gravity and the other forces (known as the double copy) and used it to turn the charged objects into black hole analogues.
They calculated the shape of the waves that rolled outward and found an expression that was surprisingly simple, and strikingly quantum.
Intrigued, O'Connell and his collaborators probed further.
The researchers had stumbled upon an unexpected pattern in the amplitude haystack.
Instead, they could stop at the five-point amplitude - which involves only a single particle of radiation.
Further calculations revealed why the five-point amplitude tells us everything we need to know about the classical world.
Quantum results have two defining features.
They have uncertainty baked into them.
Donal O'Connell, a theoretical physicist at
the University of Edinburgh.
Classical systems, such as a gravitational wave rippling through Earth, are perfectly crisp and can be described with nary a Planck's constant in sight.
These properties gave O'Connell's group a litmus test for determining which parts of which amplitudes were classical:
The group found that the simplest five-point amplitude had two "fragments,"
They then turned their attention to the no-loop six-point amplitude - the emission of two radiation particles.
This amplitude gives the wave's uncertainty, because having two radiation particles is like measuring the field twice.
In the end, O'Connell and his collaborators found that the six-point uncertainty also fell into a classical fragment and a quantum one.
In other words, the six-point amplitude had no classical information at all.
In retrospect, the result seemed somewhat inevitable.
But before investigating the fragments in detail, the researchers had naively expected that the six-point amplitude might still have some subtle classical meaning.
O'Connell had studied a force related to electromagnetism.
So to check if the result also held true for gravity, Ruth Britto at Trinity College Dublin and others used various technical shortcuts to calculate the no-loop six-point amplitude for two massive particles.
They found that it too has no classical content.
Similar logic leads the researchers to expect that at higher loops, all amplitudes with more than five points will be either all quantum, and thus ignorable, or expressible as a simpler function of known amplitudes.
An unending parade of uncertainty relationships all but guarantees it.
The upshot is that classical waves are easier to describe in the language of quantum mechanics than researchers feared.
But,
Spiraling Toward Mergers
When LIGO/Virgo picks up gravitational waves, the signal is as much as 10% noise.
Future detectors such as the space-based LISA may record ripples in space-time with 99% fidelity or better. At that level of crispness, researchers expect gravitational waves to reveal a wealth of information, such as the stiffness of merging neutron stars.
The recent progress in predicting the shape of waves using quantum amplitudes raises hopes that researchers will be able to unlock that information.
For now, though, the calculation of real, astrophysical waveforms from amplitudes remains an ambitious project.
Four- and five-point amplitudes capture what happens when black holes "scatter," or slingshot off each other, and the technique can currently be extrapolated to understand simple mergers where black holes don't spin.
But in their present state these amplitudes struggle to fully describe the more complicated mergers that gravitational wave observatories detect.
Amplitude researchers believe they can tweak their methods to calculate realistic waveforms for a wide variety of mergers, but they haven't done so yet.
Beyond gravitational waves, the general nature of the research suggests that the way the uncertainty principle organizes the quantum haystack could prove useful in other areas of quantum theory.
The infinite array of relationships between amplitudes could enable independent cross-checks, for example, providing valuable guidance for calculations that can take months.
And it may serve as a sharp test for distinguishing quantum theories that can describe our macro world from those that can't.
|