|
for
Quanta Magazine to Stephen Hawking's biggest idea - about how the universe might have come from nothing - has cosmologists choosing sides...
Stephen Hawking
chose the august setting to present what he would later regard as
his most important idea: a proposal about how the universe could
have arisen from nothing.
The Big Bang theory, for instance - pioneered 50 years before Hawking's lecture by the Belgian physicist and Catholic priest Georges Lemaître, who later served as president of the Vatican's academy of sciences - rewinds the expansion of the universe back to a hot, dense bundle of energy.
But
where did the initial
energy come from?
In 1980, the year before Hawking's talk, the cosmologist Alan Guth realized that the Big Bang's problems could be fixed with an add-on:
Inflation quickly became the leading theory of our cosmic origins.
Yet the issue of initial
conditions remained: What was the source of the minuscule patch that
allegedly ballooned into our cosmos, and of the potential energy
that inflated it?
would be like asking what lies south
of the South
Pole.
According to the record of the Vatican conference, the Cambridge physicist, then 39 and still able to speak with his own voice, told the crowd,
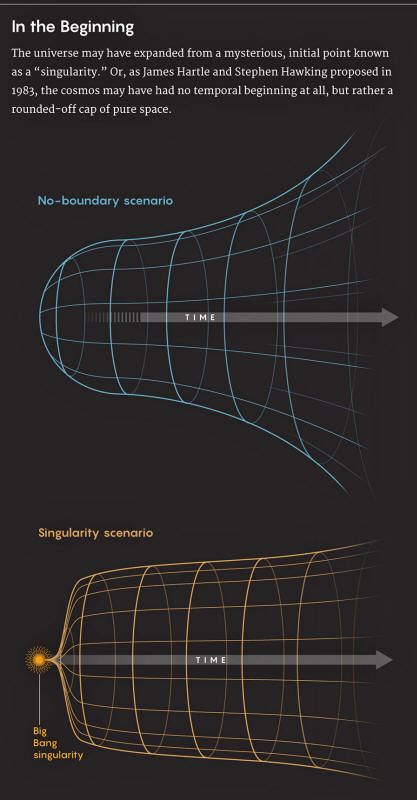
The "no-boundary proposal," which Hawking and his frequent collaborator, James Hartle, fully formulated in a 1983 paper (Wave function of the Universe), envisions the cosmos having the shape of a shuttlecock.
Just as a shuttlecock has a diameter of zero at its bottommost point and gradually widens on the way up, the universe, according to the no-boundary proposal, smoothly expanded from a point of zero size.
Hartle and Hawking derived a formula describing the whole shuttlecock - the so-called "wave function of the universe" that encompasses the entire past, present and future at once - making moot all contemplation of seeds of creation, a creator, or any transition from a time before.
at a
2014 workshop near Hereford, England.
Each moment in the universe becomes a cross-section of the shuttlecock; while we perceive the universe as expanding and evolving from one moment to the next, time really consists of correlations between the universe's size in each cross-section and other properties - particularly its entropy, or disorder.
Entropy increases from the cork to the feathers, aiming an emergent arrow of time. Near the shuttlecock's rounded-off bottom, though, the correlations are less reliable; time ceases to exist and is replaced by pure space.
As Hartle, now 79 and a professor at the University of California, Santa Barbara, explained it by phone recently,
The no-boundary proposal has fascinated and inspired physicists for nearly four decades.
The proposal represented a first guess at the quantum description of the cosmos - the wave function of the universe.
Soon an entire field, quantum cosmology, sprang up as researchers devised alternative ideas about how the universe could have come from nothing, analyzed the theories' various predictions and ways to test them, and interpreted their philosophical meaning.
The no-boundary wave function, according to Hartle,
But two years ago, a paper by Neil Turok, Job Feldbrugge of the Perimeter Institute, and Jean-Luc Lehners of the Max Planck Institute for Gravitational Physics in Germany called the Hartle-Hawking proposal into question.
The proposal is, of course, only viable if a universe that curves out of a dimensionless point in the way Hartle and Hawking imagined naturally grows into a universe like ours.
Hawking and Hartle argued that indeed it would - that universes with no boundaries will tend to be huge, breathtakingly smooth, impressively flat, and expanding, just like the actual cosmos.
Murray Gell-Mann used to ask me, ‘If you know the wave function of the universe,
why aren't you
rich?'
The trio checked their math and queried their underlying assumptions before going public, but "unfortunately," Turok said,
The paper ignited a controversy.
Other experts mounted a vigorous defense of the no-boundary idea and a rebuttal of Turok and colleagues' reasoning.
After two years of sparring, the groups have traced their technical disagreement to differing beliefs about how nature works.
The heated - yet friendly - debate has helped firm up the idea that most tickled Hawking's fancy. Even critics of his and Hartle's specific formula, including Turok and Lehners, are crafting competing quantum-cosmological models that try to avoid the alleged pitfalls of the original while maintaining its boundless allure.
The duo's theoretical
investigations of black holes and the mysterious singularities at
their centers had turned them on to the question of our cosmic
origin.
In the 1960s, Hawking and the Oxford University physicist Roger Penrose proved that when space-time bends steeply enough, such as inside a black hole or perhaps during the Big Bang, it inevitably collapses, curving infinitely steeply toward a singularity, where Einstein's equations break down and a new, quantum theory of gravity is needed.
The Penrose-Hawking
"singularity theorems" meant there was no way for space-time to
begin smoothly, undramatically at a point.
GRAPHIC: "In the ‘Beginning'"
And this led them to the shuttlecock geometry. They defined the no-boundary wave function describing such a universe using an approach invented by Hawking's hero, the physicist Richard Feynman.
In the 1940s, Feynman devised a scheme for calculating the most likely outcomes of quantum mechanical events.
To predict, say, the likeliest outcomes of a particle collision, Feynman found that you could sum up all possible paths that the colliding particles could take, weighting straightforward paths more than convoluted ones in the sum.
Calculating this "path
integral" gives you the wave function: a probability distribution
indicating the different possible states of the particles after the
collision.
The hope was that the sum of all possible "expansion histories," smooth-bottomed universes of all different shapes and sizes, would yield a wave function that gives a high probability to a huge, smooth, flat universe like ours.
If the weighted sum of
all possible expansion histories yields some other kind of universe
as the likeliest outcome, the no-boundary proposal fails.
Countless different shapes and sizes of universes are possible, and each can be a messy affair.
Of course, to actually solve for the wave function using Feynman's method, Hartle and Hawking had to drastically simplify the situation, ignoring even the specific particles that populate our world (which meant their formula was nowhere close to being able to predict the stock market).
They considered the path integral over all possible toy universes in "minisuperspace," defined as the set of all universes with a single energy field coursing through them: the energy that powered cosmic inflation.
(In Hartle and Hawking's
shuttlecock picture, that initial period of ballooning corresponds
to the rapid increase in diameter near the bottom of the cork.)
These rival universe
shapes anchor the two sides of the current debate.
probably had the best intuition of anyone on these topics.
But he wasn't
always right.
Following an initial spurt of cosmic inflation from size zero, these universes steadily expand according to Einstein's theory of gravity and space-time.
Weirder expansion
histories, like football-shaped universes or caterpillar-like ones,
mostly cancel out in the quantum calculation.
Density variations form
an inverted bell curve, where differences between regions approach
not zero, but infinity. If this is the dominant term in the
no-boundary wave function for minisuperspace, then the Hartle-Hawking
proposal would seem to be wrong.
If the dominant histories are two locations on a map, megacities in the realm of all possible quantum mechanical universes, the question is which path we should take through the terrain.
Which dominant expansion
history, and there can only be one, should our "contour of
integration" pick up? Researchers have forked down different paths.
In their view, the only sensible contour is one that scans through real values (as opposed to imaginary values, which involve the square roots of negative numbers) for a variable called "lapse."
Lapse is essentially the height of each possible shuttlecock universe - the distance it takes to reach a certain diameter. Lacking a causal element, lapse is not quite our usual notion of time. Yet Turok and colleagues argue partly on the grounds of causality that only real values of lapse make physical sense.
And summing over universes with real values of lapse leads to the wildly fluctuating, physically nonsensical solution.
He and Hartle analyzed the issue of the contour of integration in 1990. In their view, as well as Hertog's, and apparently Hawking's, the contour is not fundamental, but rather a mathematical tool that can be placed to greatest advantage.
It's similar to how the trajectory of a planet around the sun can be expressed mathematically as a series of angles, as a series of times, or in terms of any of several other convenient parameters.
He and his colleagues argue that, in the minisuperspace case, only contours that pick up the good expansion history make sense.
Quantum mechanics requires probabilities to add to 1, or be "normalizable," but the wildly fluctuating universe that Turok's team landed on is not.
That solution is nonsensical, plagued by infinities and disallowed by quantum laws - obvious signs, according to no-boundary's defenders, to walk the other way.
a challenge to Hartle and Hawking's "no-boundary" proposal
nd
floated a competing quantum description of the universe.
To team Hartle-Hawking, the critics are invoking a false notion of causality in demanding that lapse be real.
According to Hertog, Hawking seldom mentioned the path integral formulation of the no-boundary wave function in his later years, partly because of the ambiguity around the choice of contour.
He regarded the normalizable expansion history, which the path integral had merely helped uncover, as the solution to a more fundamental equation about the universe posed in the 1960s by the physicists John Wheeler and Bryce DeWitt.
Wheeler and DeWitt - after mulling over the issue during a layover at Raleigh-Durham International - argued that the wave function of the universe, whatever it is, cannot depend on time, since there is no external clock by which to measure it.
And thus the amount of energy in the universe, when you add up the positive and negative contributions of matter and gravity, must stay at zero forever.
The no-boundary wave
function satisfies the Wheeler-DeWitt equation for mini-superspace.
Hawking sought a
holographic description of a shuttlecock-shaped universe, in which
the geometry of the entire past would project off of the present.
But Turok sees this shift
in emphasis as changing the rules. In backing away from the path
integral formulation, he says, proponents of the no-boundary idea
have made it ill-defined. What they're studying is no longer Hartle-Hawking,
in his opinion - though Hartle himself disagrees.
But instead of one shuttlecock, it envisions two, arranged cork to cork in a sort of hourglass figure with time flowing in both directions.
While the model is not yet developed enough to make predictions, its charm lies in the way its lobes realize CPT symmetry, a seemingly fundamental mirror in nature that simultaneously reflects matter and antimatter, left and right, and forward and backward in time.
One disadvantage is that the universe's mirror-image lobes meet at a singularity, a pinch in space-time that requires the unknown quantum theory of gravity to understand.
Boyle, Finn and Turok
take a stab at the singularity, but such an attempt is inherently
speculative.
The proposal, which
differs from the no-boundary wave function primarily by way of a
minus sign, casts the birth of the universe as a quantum mechanical
"tunneling" event, similar to when a particle pops up beyond a
barrier in a quantum mechanical experiment.
The no-boundary wave function, for instance, favors empty universes, whereas significant matter and energy are needed to power hugeness and complexity.
Hawking argued that the vast spread of possible universes permitted by the wave function must all be realized in some larger multiverse, within which only complex universes like ours will have inhabitants capable of making observations. (The recent debate concerns whether these complex, habitable universes will be smooth or wildly fluctuating.)
An advantage of the
tunneling proposal is that it favors matter- and energy-filled
universes like ours without resorting to anthropic reasoning -
though universes that tunnel into existence may have other problems.
Or perhaps, instead of a South Pole-like non-beginning, the universe emerged from a singularity after all, demanding a different kind of wave function altogether.
Either way, the pursuit will continue.
The question of the wave function of the universe,
|