|
CONVERTING EM FIELD ENERGY TO G-FIELD ENERGY AND VICE VERSA. SLIDE 29
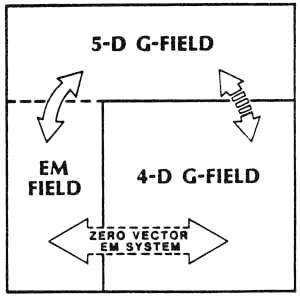
According to Kaluza theory, there are no such things as a separate EM field and a separate gravity field. Instead, in five dimensions there is only one field: the 5-d gravitational field. The EM field is the 5th dimensional aspect, while our normal 4-dimensional G-field is the other aspect of the 5-field, in our normal 4-space. Thus we may say that the 5-field is composed of two components: the 5th dimensional component (our normal EM field) and the component occupying our normal 4 dimensions (our normal G-field). The 5-d "force" field, of course -- or the 5-space analogy to a force field -- would be due to a gradient or "bleed-off" of the 5-d gravitational potential. This gradient in turn is composed of two components: the 5th dimensional "bleed-off" outside our normal 4-space (this outer bleed-off is our normal EM force field) and the bleed-off inside our normal 4-space (this inner bleed-off is our normal G-field). Normally the 5-potential bleeds-off outside our 4-space as EM field, far greater than it bleeds-off inside our world as G-field. Between two electrons, for example, the electric field is about 10 to the 42 times as strong as the G-field. Since in the Kaluza view there is only one 5-d G-potential that is causing both force fields, this shows that there is an incredibly greater EM bleed-off of the 5-potential between the two electrons than there is a G-field bleed-off between them. As shown on the diagram, the 5-d G-field is normally comprised almost entirely of the 5th dimensional EM field. Only a small 4-space G-field component exists. However, suppose we were to "block" the bleed-off of the 5-potential in the EM mode. Then none of the 5-potential could bleed-off in the 5th dimensional EM field. Instead, it would be forced to bleed-off into the 4-space G-field. In our two electron example, this "perfect case" would result in the disappearance of the E-field between the two electrons, and the G-field between them would increase to about l0 exp42 times its normal strength. The end result would be that, by blocking the EM force field bleed-off, EM field is converted to G-field. In addition, EM field energy is converted to G-field energy. With the extremely amplified gravitational and inertial effects that result, one can now accomplish direct engineering of gravitation, mass, and inertial effects. We can effectively accomplish this "blocking the EM bleed-off" by opposing EM force fields so that they sum to vector zero. This is the same as summing various 5th dimensional gradients of the 5-potential to a zero vector resultant. In that case, as much "EM bleed-back to 5-potential" occurs as there is "EM bleed-off from 5-potential." This places the 5-potential in equilibrium with respect to EM bleed-off. Also, another nice thing results: Since we can readily vary the magnitudes of the EM force field components of the vector zero summation, we can actually form phased "zero vector waves" by increasing and decreasing the magnitudes of all the component EM vectors in phase, but retaining their vector summation always equal to zero. In that case we have produced a very simple 5-space G-potential wave, which concomitantly forces phase-locked variations in the 4-space G-potential. In short, we have produced an electrogravitational (EG) wave, or scalar EM wave for short. This wave described is the simplest EG scalar wave we can produce; much more complex EG waves can be produced and used for highly specialized purposes. The scalar EG wave changes EG potential energy into 4-gravity potential energy in one half-cycle, and changes 4-G potential energy into EG potential energy in the other half-cycle. However, the EG potential energy in the first half-cycle does not react electromagnetically in linear circumstances, since it is electromagnetically a linear vector zero. So our scalar EG wave actually oscillates energy back and forth between a locked-in 5th dimensional EM potential and a 4-space G-potential. As can be seen, to the linear 4-space observer this scalar EG wave appears as a purely gravitational wave, with G-potential magnitude varying in a wavelike manner. |