|
SCALAR RESONANCE SLIDE 34
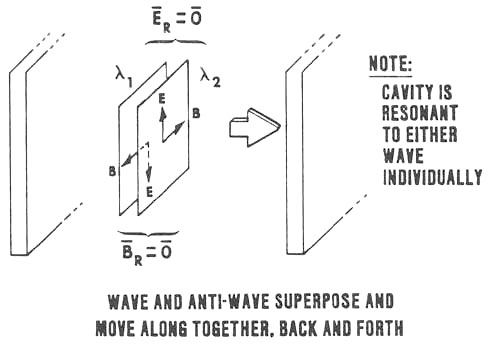
Here we explain a new kind of resonance: scalar EH resonance, or electrogravitational resonance. First, imagine we have a standard resonant cavity, represented by the two walls in our diagram. In this cavity we have a resonant EM wave moving back and forth, represented by the forward-most plane. In accordance with convention, we show the E-field vector and the B-field vector at right angles in this moving wave front. As the wave front moves back and forth, the vectors vary back and forth; however, at any one point between the walls, the two vectors always have the same value. Thus our resonant EM wave forms a standing wave in the cavity. Now imagine that a second wave front, precisely like the first and of the same frequency, is superposed over the first wave front and travels along with it. This second wave -- the "antiwave" -- has its force vectors 180 degrees out of phase with the force vectors of the reference wave. Hence the E-fields and B-fields of the two superposed waves always sum to vector zeros, anywhere in the cavity. To an external observer, the cavity contains no ordinary electromagnetic force fields, hence no ordinary EM energy. However, the energy density of a single EM sine wave in vacuum is given by
This energy density is always positive. Hence the energy density of the two waves at any point x between the walls is equal to
where
Thus the energy density of vacuum varies with x. But, rigorously, since the resultant E and B fields are zero, this describes a standing gravitational wave. Hence we have a standing EG wave, existing in the resonant cavity. This is an example of scalar resonance. Rigorously the cavity has mass and inertia, to an outside observer, as a result of the two warps in spacetime it contains. Note that in one half-cycle the energy density of vacuum is greater than ambient, and in the other half-cycle it is less. In the region of one half-cycle, time flows at a faster rate than to the ambient observer, and in the other half-cycle time flows at a slower rate than to the ambient observer. One half-cycle appears to contain negative electrical charge, and the other appears to contain positive charge. One half-cycle appears to contain a north pole (positive magnetostatic scalar potential), and the other half-cycle appears to contain a south pole (negative magnetostatic scalar potential). Perhaps now one can begin to understand why a continuously accelerated orbital electron in the atom does not radiate EM energy, completely in violation of Maxwell’s equations. The electron is naught but a complex aspect of a standing scalar resonance, existing between the nucleus and the orbit. |