The scribes clearly understood that the mechanism of eclipses has to do with the intersecting cycles of the moon and sun. The explanation of eclipses likely current when the Codex was compiled is preserved in a post-Conquest manuscript, the Book of Chilam Balam of Chumayel: ⁽¹⁾

[T]he Sun is bitten into. What bites into it, is that it is matched with the Moon, which goes attracted by it (the Sun), before biting it. It arrives through its path to the north, large, and then they become one and the Sun and Moon bite each other, before arriving at the "trunk of the Sun." It is explained this way so that Maya men can understand what happens to the Sun and to the Moon. (Katun chapter).

Not surprisingly, Maya priests had no difficulty grasping the European theory of eclipses when it was explained to them.  The Book of Chilam Balam of Chumayel recounts the pre-Conquest explanation of eclipses "so that Maya men can understand what happens to the Sun and to the Moon", then adds immediately that in fact: "Eclipse of the Moon. It isn't that it is bitten. It is interposed with the Sun, at one side of the Earth. Eclipse of the sun.

It isn't that it is bitten. It is interposed with the Moon, at one side of the Earth". But  Maya astronomy was primarily concerned with augury, ritual, and mythology, not scientific investigation of the heavens. Eclipses were regarded as ominous portents throughout Mesoamerica.  According to the Florentine Codex, the Aztecs believed a malevolent deity called Tzitzimime descended from the sky during eclipses.

His Maya counterpart may be illustrated in the Dresden Codex.  J. Eric Thompson ⁽²⁾ published a letter received from a native friend in Belize concerning a lunar eclipse in July, 1935 which shows that trepidation about eclipses survived into recent times:

On the night of the 15th-16th of this month an eclipse of the moon was seen. All the people were frightened, saying the world would end that night. A lot of noise was made beating tin cans, boxes and bells. [There were] prayers and processions in the night at one o'clock. All were awake [believing] that was the moment of the [last] judgement.

Eclipses were also a tool for prognostication. The Book of Chilam Balam of Tizimin ⁽³⁾, recalling what must have been an older tradition, lists eclipse augury among the ways of predicting the future:

At the time of seeking fire, of seeking shark tails. That is the return of the seeking of things, when one seeks them in the sky, in storms, in sun phases, far seeing, at the time of the covering of the face of the sun, of the covering of the face of the moon [which recurred] on the fourteenth tun again [1607 AD]. (folio 5r)

Maya astronomy was shaped by a cyclical concept of time. Before the conquest, priests and scribes manipulated a complex set of interlocking  cycles that measured time from creation of the present world to its eventual dissolution. The most important cycles were combined in the Maya calendar.

A 260 day ritual cycle, the tzolk'in, interlocked with a 365 day year, the haab. A combined date in these two cycles repeated only every 52 years, the length of the calendar round. This was in turn synchronized with the long count that measured off time from the creation of the world. By determining the place of each day in these cycles, its character could be predicted.

As David Carrasco observed in Religions of Mesoamerica ⁽⁴⁾

The Maya were deeply concerned to locate all events . . . within a cosmological framework designed to insure the regeneration of life. . . . Time past and time future were fixed in a discernible pattern that could be read and predicted. In addition to this nearly five-thousand year cycle [of the calendar] were a series of other cycles, which the Maya marked, celebrated, and sometimes feared in detail. 

Maya astronomy sought to discover the patterns of celestial motions, and make them commensurate with the calendar. The eclipse table in the Dresden Codex tracks through 405 lunar months, 11,959 days according to the reckoning in the table.

This is one day short of 46 complete tzolk'in cycles.  With a one-day correction, the table will recover the initial tzol'kin date.  Accurate observation was required to carry out the table to this length without significant error. According to modern measurement, 405 lunations equals 11,959.89 days.

The average value of the lunar month implied by the table is thus correct to within 7 minutes.

Familiarity with the Maya calendar is a prerequisite to a proper understanding of the eclipse table.

Click on the image at the left for a brief  Note on the Maya Calendar, where you will also find links to more detailed discussions of the calendar. 

Despite their abilities as observers, the scribes were sometimes willing to sacrifice accuracy in order to make cycles commensurate. They were also limited by the simple naked-eye techniques available to them. The eclipse table itself appears to do no more than identify "warning stations", times at which eclipses might occur, at which appropriate rituals would be required.

However, it is not the accuracy of Maya astronomy so much as its ambition to capture the cycles of the heavens in an all-embracing  framework of sacred time that is remarkable. The magnificent  structure erected by Maya astronomers should not be reduced to a mechanical system, a primitive (and therefore less successful) version of modern positional astronomy. 

As Anthony Aveni ⁽⁵⁾ has written:

The Maya integrated and interrelated the properties of things they captured in their universe of senses... I further assume that the processes of interrelation, which are manifest in so many aspects of the material remains of the Maya, were sophisticated, complex, well thought out and in nearly all cases very different from our positivist taxonomies, cause-and-effect explanations, and functional principles of association. 

I believe their acuity in sensing the phenomena they transformed into their symbolism was sharper than our own, and that it was capable of revealing patterns of behavior in nature not yet known to us, for they were conditioned by a life-time of immersion in particular sights, smells, and sounds that nourished their sensual appetites, a lifetime unencumbered by the dulling of direct sensual perception that results from the intervention of technology.

The Dresden Codex

The Dresden Codex is one of only four surviving Maya hieroglyphic books painted on white-limed bark paper.  Friar Diego de Landa, writing in about 1566, reported that  "we found a great number of books... and since they contained nothing but superstitions and falsehoods of the devil we burned them, which they took most grievously, and which gave them great pain".⁽⁶⁾

If the good brother's crime of book burning could be excused by his religious zeal, he might be able to claim some justification.  The codices have been described as priest's handbooks, used to time rituals and make auguries.

The Dresden Codex survived the fires of the Spanish friars because it was sent to Europe as an example of native art. It may have been sent to King Charles V by Cortes himself.  But the Spanish were more interested in gold than pagan art. The Codex eventually found its way to the Dresden public library, where it gathered dust until it was rediscovered in the late 19th Century by the library archivist, Ernst Forstemann.
 

View Andreas Ful's photographic reproduction of the  eclipse table on-line at his Dresden Codex web-site. For information about other on-line and print editions of the Dresden Codex, see the note on the Codices page at this web site.

Note on page numbers:  Some time before Forstemann studied the Codex, it fell apart into two pieces that were improperly rejoined. Forstemann's edition numbers the Eclipse table pages 51-58. 

These pages numbers were kept in most later editions, but the correct numbering is 30-37.

The structure of the eclipse table

The eclipse table occupies pages 51 to 58 of the Codex. Each page is divided into upper and lower sections by a horizontal red line.

The Codex is read across the top halves of  the pages, usually designated 51a to 58a. The table then continues on the lower halves of the pages, from 51b to 58b. Pages 51a and 52a contain long count dates for entry into the main part of the table and a table of multiples.

The eclipse table proper,  a listing of "eclipse warning stations" begins on 53a.
 
 

The table of eclipse warning stations

Solar eclipses occur at new moon, when the moon is between the earth and sun. Lunar eclipses occur at full moon, when the earth is between the sun and moon.

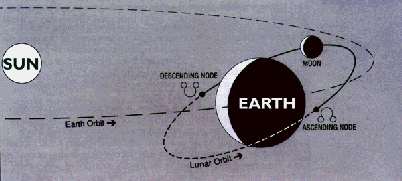
Eclipses would occur every month if the moon's orbit was not inclined slightly to the ecliptic,  the plane of the earth's orbit.  Eclipses are possible only when the moon is near a node of its orbit, that is, on the ecliptic.

The moon's orbit crosses the ecliptic twice, at the "ascending node" and "descending node". 

It is important to note that the orientations of the moon's orbit at intervals of about half a year (when the earth/moon system is on opposite sides of the sun) are mirror images of one another.

Thus if  the moon is near the ascending node at the time of an eclipse, it will be near the decending node about half a year later.  There is a good chance that an eclipse will repeat at the new or full moon nearest this time. This will usually be six  lunar months, 177 days, after the first eclipse. Several eclipses may follow at 177 day intervals, but the moon is further from the node at each repetition, and eventually strays too far from the node for an eclipse to occur.

At the time of the last eclipse in a series, the closest new or full moon to the node may arrive after five lunar months, 148 days, rather than six.  Here, then,  is the pattern that led Martin Meinshausen to the conclude that the Codex predicts eclipses.

If the nodes were stationary, the sun would align with a node every six calendar months. But the nodes slowly slip about the moon's orbit, making a complete circuit in 18.61 years. This phenomenon, "recession of the nodes", reduces the time between eclipse seasons. The sun is actually aligned with a node at 173.31 day intervals.

In consequence, if an eclipse occurs exactly at the node, the new or full  moon 177 days later occurs four days after alignment, and after each suceeding 177 day interval, the moon is four days further still from the node.  Eclipses are possible  until the moon is more than 18.75 days from the node. A series of 7 or 8 solar eclipses, the first on one side of a node, the last on the other,  is possible. 

Note  that at the end of an eclipse series, the moon will be more than half a lunar month from the node at the end the last interval of six lunar months. Thus the moon will be closer to the node at the fifth lunar month, 148 days,  rather than the sixth.  Therefore, the last eclipse will occur only 148 days after the next the to last.  The average time between eclipse warning stations in the Codex is 173.32 days, almost exactly the length of the "eclipse half-year". 

The sequences of 177/148 day intervals predict only the possibility of an eclipse.  All the eclipses in a series will not be visible at the same location. Solar eclipses are visible only along narrow eclipse tracks on the surface of the earth. Lunar eclipses are visible only if the moon is above the horizon at the time of the eclipse.

See What Causes an Eclipse?   for a good elementary tutorial on solar and lunar eclipses 

Robert Willson discovered that the Codex also makes longer range eclipse predictions. The time required for the moon to move about its orbit from ascending node to ascending node is the draconic month, 29.21222 days.  The time between new moons is the synodic (lunar) month, 29.53059 days. 

Because the moon must be near a node at the time of new or full moon for an eclipse to occur, eclipses repeat after any interval that is both an integral multiple of synodic months and an integral multiple of  draconic months or half draconic months.  The best known example from Old World astronomy is the Saros = 38 draconic months = 35 synodic months = 6585.32 days. 

The days elapsed between pictures in the Dresden eclipse table are not explicitly recorded,  but Willson found them interesting.   Each total (except the last) is one of 1034, 1210, 1565, or 1742.  These are all recognized "eclipse cycles". 

The eclipse cycles recorded in the Dresden are shorter than the Saros, but no less valid.  Recurrence of an eclipse at eclipse cycle intervals is virtually certain, though the second may not be visible to the observer who recorded the first.

See the on-line Catalog of Eclipse Cycles  for discussion of cycles identified by ancient and modern astronomers.

Willson realized that the pictures in the table could be either eclipse warning dates or an historical record of eclipses visible in the Yucatan. However, he rejected the latter hypothesis after failing to match the intervals between the pictures in the table with any sequence of solar eclipses actually visible in the Yucatan from the l^st to 15^th centuries.

He also noted that the table appears to have some leeway for prediction built into it.  A column of three consecutive tzolk'in dates is recorded below each cumulative total in the table.

Willson suggested that the column of consecutive dates implies a ±1 day latitude in the table.

Maya lunar astronomy dates back to the early Classical period, if not earlier. Long count dates on classical monuments are often followed by "lunar series" glyphs that give the age of the moon (the time since new moon). The earliest example, on a monument from Uaxactun, dates to  397 AD, but a vase from the same site hints that the lunar calendar was already in use in 42 AD. The moon age on many monuments appears to have been calculated by adding multiples of lunar months to a base date.

The 177 days = 6 lunar months formula used in the Codex was known to Classical scribes. The inscription on the Temple of the Sun at Palenque, dedicated in 692 AD, appears to use the formula 81 lunar months = 2,392 days, which gives an average length of the lunar month identical to the average calculated from the Codex formula of 405 lunar months = 11, 960 days.

It is also  possible that the Maya deduced one of the critical factors in eclipse prediction, the recession of the nodes, from lunar observations. During the 18.61 years required for the nodes to regress about the lunar orbit, the position of the moon on the horizon when it rises also shifts.

In the tropics, the variation in the azimuth limits of moon rise is about 10 degrees over the course of the cycle. Thus recession might have been discovered without accumulating a long record of eclipses. There is some evidence that Mesoamerican observers did keep track of the azimuth of moon rise, but it is inconclusive.

See Lunar Astronomy in the Inscriptions  and David Dearborn, To The Limits: A  note on lunar precession in Mesoamerican astronomy

Using the table

The eclipse table will work reasonably well if  it is entered on  the date of any eclipse, or even on the date of a new or full moon that occurred reasonably close to a node.  Each interval of 177 or 148 days counted from the initial date would reach a "warning station" at which an eclipse might occur. Both solar and lunar eclipses could be predicted in this way.

If, for example, the initial date was a new moon at which a solar eclipse occurred, the warning stations would predict solar eclipses, but the full moons in the same lunar months would be times when lunar eclipses might occur.

It is quite possible that the eclipse table was used in this way, but the tzolk'in dates listed in the table suggest that the table was intended for use from a particular date. The central date in the column of day signs in the first entry in the table (page 53a) is 7 Chikchan. A cumulative total intended to read 177 is recorded above. This suggests that 7 Chikchan is reached after a count of 177 days from an initial entry point.

This is a day 12 Lamat. Once again, the table would work as at least a rough eclipse warning system if entered on any 12 Lamat in the  tzolk'n cycle at a  new or full moon close to a node, but the Codex supplies at least one 12 Lamat entry point that is fixed in time by linking it to a long count. This is  the long count 9.16.4.10.8 12 Lamat,which correlates to 12 November 755 AD.

A new moon did occur on this date. However, this could not have been the entry date used by scribes who consulted the Dresden Codex to predict eclipses.  755 AD  is 500 years earlier than the date on which the Codex was written.

Thus it is usually assumed that a later 12 Lamat that also fell on a new moon was the practical base date for eclipse predictions.

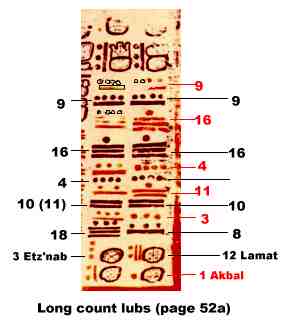The 755 AD entry date is found in the last two columns of glyphs on page 52a. There are actually four long count numbers here, two are included in each column, intertwined in red and black. The second column date in black is 9.16.4.10.8 12 Lamat. 

The number in red is 9.16.4.11.3 1 Akbal, just 15 days later. The black number in the first column is almost certainly intended to be 9.16.4.11.18 3 Etz'nab, 30 days later than 12 Lamat. (It actually reads 9.16.4.10.18  3 Etz'nab, but this long count does not reach a tzolk'in date of  3 Etz'nab.The winal coefficient must be 11, rather 10, to reach 3 Etz'nab).

9.16.4.10.8  12 Lamat  date is apparently the principal entry point into the table.  Since this date was close to the time of a new moon, the tzolk'in dates in the table thus predict solar eclipses.

Most students of the table interpret the second and third dates as secondary entry points used concurrently with 12 Lamat.  The second long count date provides a entry point that occurs near the time of a full moon. The table will count from this date to lunar eclipse warning stations 15 days after the tzolk'in dates in the table.

The third date falls on the next new moon, and is presumably a secondary entry point for predicting solar eclipses. ⁽⁸⁾

If the primary entry point is at the node, the secondary solar eclipse predicting entry point will not supply as many successful predictions as the primary entry point. For this reason, Teeple⁽⁹⁾ and Lounsbury⁽¹⁰⁾ rejected the notion that the second and third dates function as concurrent entry points.  However, in 755 AD, the node was closer to the lunar eclipse predicting entry date than to the 12 Lamatentry date.

Thus eclipses were possible at warning dates counted from either of the solar eclipse entry dates. While this increases the number of  warning dates without eclipses, it is likely that failure to predict an eclipse was a more serious matter than predicting one that did not occur.  It should also be noted that even an entry at the node will predict more eclipses that are not visible in the Yucatan than visible eclipses.

The fourth long count on page 52a (the red number in the first column) contains an error that cannot be easily corrected. The count does not reach the 7 Lamat tzolk'in date written below it.

The function of this number is unknown.

More about the classical base date

9.16.4.10.8 12 Lamat (12 November 755 AD) may have been the base date of a Classical predecessor to the Dresden eclipse table. If it was used as a practical entry date into the table,  the date must have been a new moon within 18 days of a node passage. In fact, new moon occurred near mid-day in the Yucatan on 12 November 755.

The moon passed through the node about two weeks later, near the time of the 1 Akbal lunar eclipse entry date,  and a lunar eclipse occurred near this date.  A partial solar eclipse followed a month later, near the 3 Etz'nab secondary solar eclipse entry date.

Neither of these eclipses were visible in the Yucatan, but this does not diminish the utility of the table as a warning system pointing to possible eclipses at later dates. It might also be noted that a total lunar eclipse was visible in the Yucatan 177 days earlier than the lunar eclipse predicting 1 Akbal entry date.

Harvey and Victoria Bricker have shown that all 77 solar eclipses (including many not visible in the Yucatan) in the 33 year run of the table from 9.16.4.10.8 12 Lamat occurred within two days of the warning stations counted from the primary or secondary solar eclipse predicting entry dates⁽¹¹⁾.

Aveni has shown that the lunar eclipse entry date works almost as well. 51 of the 69 lunar eclipses in the 33 year life of the table are within one day of warning stations.⁽¹²⁾

Except as otherwise noted, the "85" version of the GMT correlation between the Maya long count and the Gregorian calendar is used here. This places the "zero" long count on 13 Aug 3114 BC. However, the "83" version, which places the beginning of the count on 11 August is preferred by many Mayanists. The "84" version which begins the count on 12 August was once widely accepted, but has fallen into disfavour. 

The mean error in predicting solar eclipses if the "85" correlation is used is only .08 days. However, the Brickers prefer the "83" correlation, which makes the mean error 1.92 days. Nevertheless, the choice of correlation may not be as critical as it might seem in interpreting Maya astronomical tables. For example, new moon occurred near noon 12 November 755,  9.16.4.10.8 12 Lamat according to the "85" correlation.

But if the scribes fixed the date of new moon at midnight, the new moon could as easily been assigned to 11 November,  which is 12 Lamat in the "84" correlation. Finally,  the instant of the astronomical new moon is the moment of conjunction between the moon and sun, which cannot be observed directly. The scribes may have fixed it to the time when the old moon disappeared. This could well have led to 10 November as the date of the new moon, which is 12 Lamat in the "83" correlation.

In addition, the three day window at each warning station further obscures differences in the correlation.

The Brickers believe that  9.16.4.10.8 12 Lamat was actually used to predict eclipses in a Classical eclipse table that was copied by the scribes who composed the Dresden Codex.  Many scholars disagree. Floyd Lounsbury argues that 9.16.4.10.8 12 Lamat is likely a "throw back", calculated by subtracting whole multiples of the table length from a more accurate, but unrecorded, base closer to the time when the Codex was written.⁽¹³⁾

The problem with accepting 9.16.4.10.8 12 Lamat as a practical entry date is that it is nearly 15 days from a node of the moon's orbit, and thus only minimally acceptable as an eclipse predictor. In fact, more of the solar eclipses that occurred in the 33 years following 9.16.4.10.8 12 Lamat match with warning stations reached by counting forward from the 3 Etz'nab secondary entry point rather than from the 12 Lamat primary entry.

Cumulative error when the table was projected back in time several centuries would explain why the Classical entry date is not an optimal choice.

See the on-line catalogs of  eclipses: World Solar Eclipses 1001 BC - 2500 AD  Solar Eclipses Visible in Mesoamerica AD 1 to 1600
World Lunar Eclipes 1001 BC - 2500 AD  and  Lunar Eclipses Visible in Mesoamerica AD 1 to 1600

A throw back entry point is not a fanciful idea. There are dates in the DresdenVenus table that are more clearly throw backs. In addition, the eclipse table itself contains what appears to be a throw back to the date of the first new moon after creation of the world.

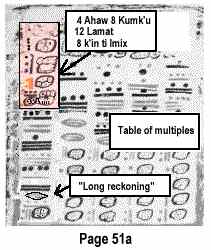
The first column on page 51a reads in part 4 Ahaw 8 K'umku 12 Lamat 8 k'ins ti Imix, followed by intertwined black and red numbers and 12 Lamat again. 4 Ahaw 8 K'umku is the calendar round date of creation, the beginning of the long count. 

Thompson suggested that 8 k'ins ti Imix implies counting eight days in the direction of Imix (the day following Ahaw) from creation (the beginning of the long count on 4 Ahaw 8 K'umku 0.0.0.0.0) to 0.0.0.0.8 12 Lamat,the presumed first new moon.The black number written above 12 Lamat is what Thompson called a "long reckoning", apparently intended to read 9.16.4.10.0 .

If this is added to 0.0.0.0.8 12 Lamat, the resulting long count position is the 9.16.4.10.8 12 Lamat entry point into the table.⁽¹⁴⁾

^{The numbers and tzolk'in dates in the first column of page 51a follow the  format of  "ring numbers" found elsewhere in the Codex. This is why Thompson was confident in suggesting that the first coefficient of the  black "long reckoning" should read 9 rather than the 8 recorded by the scribe. For an on-line tutorial on ring numbers, see Gregory Reddick, Ring and Serpent Numbers in the Dresden Codex.}

Lounsbury suggested that 9.16.4.10.8 12 Lamat may have been calculated as a theoretical entry date because it is the earliest 12 Lamat that produces predictions accurate enough to make the table useful. However, it is likely that throw backs have augural or ritual purposes.  Because Mayan scribes conceived of time as cyclical, historical intersections between cycles provided the basis for prediction of future events.

For example, the Chilam Balam of the post-Conquest era was responsible both for  predicting the fate of the coming katun from knowledge of events in past katuns that began on the same tzolk'in date, and for recording events for the benefit of his successors.

Information about astronomical and perhaps other events that coincided with the eclipse cycle presumed to begin on 9.16.4.10.8 12 Lamat may be imbedded in the eclipse pages. For example, Closs notes that the 32nd eclipse station in the table is dated to 9.17.0.0.0 13 Ahaw, when an eclipse was actually visible in the Yucatan. Since this is the only case in Maya history in which an eclipse coincided with a katun end, it was likely regarded as particularly significant. It is also memorialized on both Quirigua Stela E and in the Paris Codex.⁽¹⁵⁾

It is also possible that the  9.16.4.10.8 12 Lamat base date was attached to the table to preserve links with other material in the Codex. Aveni has shown examples of eclipse cycles imbedded in the Venus table.⁽¹⁶⁾

Hofling has pointed to eclipse imagery in the illustrations accompanying auguries in the Moon Goddess almanacs (pages 16-23 of the Codex), and has demonstrated that some intervals in the almanacs correspond to the eclipse cycles in the eclipse table. ⁽¹⁷⁾

Recycling the table

After a complete run through the table, it can be re-entered after a lapse of one day on another 12 Lamat. Evidence that the almanac was intended to be recycled is provided by a table of multiples of 11,960 (1.13.4.0) on pages 51a and 52a. As Thompson notes, there are some "irregularities" in the table, but its general purpose is clear.⁽¹⁸⁾

Below the table of multiples, tzolk'in dates are listed. The first three rows repeat 12 Lamat, 1 Akbal, and 3 Etz'nab respectively, the tzolk'in dates on which an almanac cycle can begin.

Although the table can be recycled, error accumulates with each re-use. Because the 11,960 day cycle from 12 Lamat to 12 Lamat is 0.11 day longer than 405 lunations (= 11,959.89 days), the time of the new moon is shifted by 0.11 days after one cycle through the almanac. After 8 passes, the entry date will be a full day from the time of new moon.  A more serious problem affects the warning stations at 177/148 day intervals.

These function as eclipse warning dates because the eclipse half-year (6 draconic months) is between 5 and 6 lunar months long. But 11,960 days is about 1.6 days longer than a whole multiple of the eclipse half-year. This means that the warning dates are displaced by this amount in the second use of the table.

In 1930, J. E. Teeple showed that the warning dates may have remained useful for longer than the calculation above suggests. He noted that when the tzolk'in warning days (including both the central date and those ±1 one day from it) are plotted on a double tzolki'n , they cluster in three groups of dates that are equally spaced in the 520 day cycle, marking distinct "eclipse seasons", each about 32 days long. This is a consequence of the fact that two tzolk'in cycles are very close to three eclipse half-years.

The table will still produce dates within the collective warning zones for about 5 cycles through it.⁽¹⁹⁾

Teeple's eclipse seasons hypothesis assumes that the entry date on the initial run through it is centred on the node. One of the reasons Teeple rejected 9.16.4.10.8 12 Lamat as a practical entry date is because it is nearly 15 days from the node. However, the Brickers suggest that eclipse seasons may have been calculated from the 1 Akbal and 3 Etz'nab entry dates as well.

Since the 1 Akbal lunar eclipse predicting entry date was close to the node, it fits Teeple's requirements. When the eclipse seasons calculated from all three entry dates are combined,  the warning seasons are rather too long to be practical, but the Brickers note that actual eclipses in the 33 years following 9.16.4.10.8 12 Lamat are concentrated in the centres of these seasons. They believe that narrower eclipse-season limits were fixed by observation.⁽²⁰⁾

The Dresden Venus table includes a method for correcting accumulated error in successive passes through it. This suggests that a correction scheme may also have been applied to the eclipse table.  Teeple showed that the error in the eclipse seasons that accumulated after five cycles through the table could be corrected by moving the 148 days entries 1 column forward.

The Brickers note that a short-term correction can also be made by re-entering the table a day earlier on each successive pass. Since the actual length of the table is 11,989 days rather than the 11,960 required to recover the initial tzolk'in entry point, this procedure is at least plausible. Correcting the table in this way solves the problem of the straying of warning stations, but does so at the cost of compounding the problem of cumulative error in the length of the table.

The Brickers suggested that it was used to retain maximum accuracy for five passes, after which more drastic correction would be required. Such correction methods are plausible, but as Lounsbury has observed, they presuppose that the Mayan scribes knew the rate of regression of the node, or of eclipse seasons, through the tzolk'in.

He concludes that "there is no clear evidence to indicate that they knew this, although the possibility cannot be excluded".⁽²¹⁾

Several methods of longer term correction have also been proposed, but are even less likely to have been known to the scribes. Thompson suggested a method involving foreshortening runs through the table so as to return to a 12 Lamat date before the end is reached. This approach is suggested by the Venus table, which is more clearly designed to be corrected in a similar fashion. The specific correction formula Thompson deduced was suitable only to restore accuracy to the table as a tool for calculating lunations.⁽²²⁾

The Brickers have proposed a more ambitious correction method. Although it makes use of what Thompson dismissed as the "irregularities" in the table of multiples, it involves a number of assumptions that have left most commentators unconvinced.

Aveni, though impressed by the Bricker's scheme, warns that,

"the problem of how the Maya lunar table was used is a bit like that of how Stonehenge functioned as an astronomical observatory. A multiplicity of competing models can be offered, but the uniqueness of a particular one can never be demonstrated".

A post-Classical base date?

The base date actually used to predict eclipses at the time the Dresden Codex was in use must have been later than 9.16.4.10.8 12 Lamat if acceptable predictions were expected. Presumably, this date would have been a 12 Lamat during the post-Classical era.

Whether the Classical base date in 755 AD was used in a Classical eclipse table or a calculated throw-back,  it is plausible to assume that a post-Classical base was most likely a whole number of  cycles of the length of the eclipse table later than 755 AD.

Teeple calculated that the node recedes by about 1.61 days in a passage through the table. In 755 AD, the moon was about two weeks from the node at new moon on the 12 Lamat entry date. About 10 cycles later, new moon fell close to the node on 12 Lamat. Teeple suggested that the "practical" entry date was a 12 Lamat near this time. He suggested a base date between 10.12.0.0.0 and 10.15.0.0.0 (1066-1125 AD). An entry date in this window would produce more accurate eclipse predictions than the Classical base date.⁽²³⁾

In 1943, Maud Makemson proposed 10.12.16.14.8 12 Lamat, 10 cycles through the table later than 9.16.4.10.8 12 Lamat. Using the "84" version of the correlation constant preferred by Makemson, this corresponds to 25 April 1083 AD. On that day, a near-total annular eclipse of the sun was visible in the mid to late afternoon throughout the Maya area.

Makemson also showed that if her base date is correct, pairs of partial eclipses enclosing lunar eclipses occurred at nine of the ten stations in the table marked by pictures, though few were visible in the Mayan area.⁽²⁴⁾

In 1965, Satterthwaite chose 11.6.2.10.8 12 Lamat (10-12 April 1345 AD), 18 cycles after 9.16.4.10.8 12 Lamat, as the most probable base that fits the "83" correlation constant he preferred. His second choice was earlier, 10.19.9.12.8 12 Lamat (17-19 April 1214 AD).⁽²⁵⁾ Thompson favoured the latter because it is close to the date when he believed the Codex was written.⁽²⁶⁾

The Brickers, who argue for a late date for the Codex, have revived Satterthwaite's original suggestion. By applying their correction scheme for updating the table from the recorded 9.16.4.10.8 12 Lamat  entry date, they conclude that the table was intended for use from 1266 to1375.⁽²⁷⁾

Since more evidence points to either the "85" or "83" constants than the "84" constant, doubt is cast on Makemson's conclusions. Thompson was initially convinced by Makemson's argument, but revised his opinion when he learned that pairs of solar eclipses in a single lunation are never visible at the same place.

He believed this made the pattern of eclipses discovered by Makemson irrelevant. However, if the eclipse table is concerned with recording warning points rather than actual eclipses, Thompson's objection loses validity. The pattern of eclipses identified by Makemson results from the coincidence of her base date and the node, the necessary requirement for accurate functioning of the table from any base date.

It is also worth noting that the dates given by the "84" constant are intermediate between those given by the "83" and "85" constants. Thus, whichever constant is chosen, the new moon and eclipse of 25 April 1083 AD was within 1 day of the entry date proposed by Makemson, and within the 3 day warning zone prescribed by the table.

The 9.16.4.10.8 12 Lamat base date actually recorded in the Codex is most compatible with the "85" correlation constant.  But as Lounsbury, an advocate of the "85" constant, has pointed out, almost any method of finding a plausible 12 Lamatentry date within the range favoured by Teeple and Makemson will favour the "84" constant. A later date still will favour the "83" correlation.⁽²⁸⁾

Perhaps the most serious objection to all of the proposed post-Classical entry dates is simply that they do not appear in the eclipse pages. There are, as Lounsbury has noted, many multiples of the length of the eclipse table that would produce a practical entry date if added to the 9.16.4.10.8 12 Lamat date recorded in the Codex.

Which, if any, were used by scribes and priests who consulted the Dresden Codex must remain a matter of speculation.
 
 

The illustrations and text

The illustrations on the eclipse pages are clearly eclipse imagery. The most obvious formula, repeated with minor variations in four pictures, shows a k'in sign, representing the sun, suspended between black and white lozenges, suggesting the movement of the sun through the eclipse shadow.

The lozenges themselves hang from sky bands, the iconographic representation of the ecliptic. In two cases, the k'in/lozenge is shown in the process of being swallowed by a snake. Pages  55a and 56a are illustrated with the face of the Sun God, K'inich Ahaw. 53a pictures Kisin or Yum Kimil, the death god.  On 53b, a goddess hangs by her neck from a sky band. Her body is marked with black spots, symbolism shared with the death god, and her eye is closed.

Closs notes that in Yucatec, an eclipsed body is said to have been blinded. This is likely a  moon goddess, usually identified with Ix Tab, mentioned by Landa as goddess of suicide and hanging.⁽²⁸⁾

Until Michael Closs examined the connection between Venus and eclipses, the least obvious eclipse imagery was the picture on 58b, showing a human form with the Venus glyph in place of its head, hanging by its feet from eclipse glyphs on the sky band.

This is likely the Maya equivalent of the Aztec Tzitzimime, who plunges to earth during eclipses. 

Closs reads his name in the glyphs above the illustration as Ah Tzul Ahaw, "dog lord" or "spine lord". Venus is associated in Mexican mythology with the dog who leads the sun to the underworld. This no doubt reflects the fact that Venus is never far from the sun, rising and setting near sunrise and sunset. Closs believes Ah Tzul Ahaw was regarded as a causative agent of eclipses. Ah Tzul Ahaw is also mentioned in the text on page 53a.

The dates associated with each reference (counting either from the 9.16.4.10.8 12 Lamat  entry date or the secondary solar eclipse entry date) coincide with eclipse warning stations that occurred when Venus was at maximum elongation.⁽²⁹⁾

Other astronomical information may be embedded in the the iconography of the eclipse table. The Brickers suggest that at least some of the images represent zodiacal constellations. For example, in the Paris Codex, a rattlesnake represents the constellation equivalent to Pisces in the Old World zodiac (according to the Brickers' controversial interpretation of the Maya zodiac).  They have attempted to demonstrate that illustrated eclipses occur in the constellations they identify during runs through the table from the "practical" entry dates they postulate in the 13th and 14th centuries. ⁽³⁰⁾

Felix Verbelen  points to intriguing  examples of possible records of conjunctions in the images.  For example, the Sun God  image on page 55a includes a large circular element flanked by a triad of smaller circles. On 26 March 1187 AD, a lunar eclipse was visible in the Yucatan, and Saturn, Jupiter, and the 1st magnitude star Spica formed a triad just below the moon.

Counting forward from 55a  on ths date to 54b reaches 16 April, 1204 AD, when a visible lunar eclipse coincided with conjunction of the moon with a visible double star (alpha Librae), which Verbelen believes is also recorded in an iconographic detail.  If the GMT correlation is is correct, Verbelen's series of visible lunar eclipses does not match the tzolk'in dates recorded in the table.  In consequence, he questions the GMT correlation.

However, since the table can be used from the date of any new moon close to a node, it is quite possible that the scribes embedded details of observed eclipses not counted from the recorded entry date. ⁽³¹⁾

The astronomy of the eclipse table was worked out long before anything but dates and numbers could be read with certainty in the Codex.  Thompson attempted to read the texts above pictures, but was not very successful. He expected auguries of dire events, and persuaded himself that he had found them.⁽³²⁾

In fact, the more intelligible texts seem to be more concerned with eclipse imagery. The auguries, as is often the case elsewhere in the Codex, are usually elliptical, left to be implied from the nature of deities named or from the eclipse imagery itself.

Despite the strides that have been made in decipherment of Maya hieroglyphics in the last three decades, the text of the eclipse table is still not very well understood. There are two-glyph captions above each eclipse warning station, and longer texts above each picture. The two-glyph captions are still mostly unintelligible, but the general meaning of some of the longer texts is now reasonably clear. 

One of the texts referring to Ah Tzul Ahaw translated by Closs will serve as an example.⁽³³⁾
 

ECLIPSE TABLE
.

Eclipse types: t = total solar or umbral lunar  a = annular solar eclipse p = partial solar or penumbral lunar u = partial umbral lunar
vis = visible at Tikal. The fraction of totality of solar eclipses visible at Tikal is also recorded above.  Eclipse data is adapted from Felix Verbelen's on-line cataloges:  World Solar Eclipses 1001 BC - 2500 AD  Solar Eclipses Visible in Mesoamerica AD 1 to 1600  World Lunar Eclipes 1001 BC - 2500 AD  and  Lunar Eclipses Visible in Mesoamerica AD 1 to 1600

Note on scribal errors:  The occasional addition of 178 when 177 is recorded appears to be an attempt to compensate for cumulative rounding error (6 lunar months = 177.18 days), and cannot itself be regarded as an error. 

With this adjustment (recorded in the table above by indicating a count of 177 (178)), the sequence of counts of 177, substituting 148 before pictures, contains only one error: A count of 177 is recorded before the 4th picture, rather than 148. This is indicated above as a count of 177 (148).  Note also that a count of 177 is recorded before the last picture, but this appears to be correct since it conforms to the sequence of tzolk'in dates.

The sequence of tzolk'in day numbers/names counted from entry on 12 Lamat contains only a single error. At the 18th station, the count reaches 9 Etz'nab, but is recorded as 7 Etz'nab. This is indicated above. The sequence of tzolk'in dates counts through 11959 days, which is assumed to be the true length of the table by most students.

The positions at which 178 is substituted for 177 are deduced from the counts between tzolk'in dates rather than from the cumulative totals, which contain more errors.  Note finally that some students assume that the last tzolk'in date is in error by one day. If the final count is assumed to be 178 rather than 177, the table length would be 11960 days, exactly  46 complete tzolk'ins. This would make the final tzolk'in date 12 Lamat rather than the recorded 11 Manik.

The most error-ridden portion of the table is the sequence of cumulative totals. Errors are frequent, but are usually compensated in subsequent positions in the sequence. Consider, for example, the first half page of the table (page 53a). The first total  is likely correct, 8.17 = 177 ( though it now appears,due to damage to the manuscript,  to read 7.17 = 157). The second total should be 177+177= 354, but is clearly recorded as 353. The third corrects the count. It reads 502 (= 177+177+148).

The fourth is again in error, reading 674 rather than 679 (=502+177). However, the fifth (856 =679+177) and sixth (1033= 856+177) are again correct.  Although most errors are compensated, a final error brings the last cumulative total to 11958 rather than 11959. No effort has been made above to indicate errors in the cumulative totals.

The totals set out above are corrected to conform to the sequence of tzolk'in dates.
  

References

1. Anthony F. Aveni. Skywatchers. Univ. of Texas, 2001 (revision of Skywatchers of Ancient Mexico).

2. "The Real Venus-Kukulcan in Maya Inscriptions and Alignments". Sixth Palenque Round Table, 1986. eds. Robertson and Fields, U Okla, 1986

3. "The Moon and the Venus Table: An Example of Commensuration in the Maya Calendar", in Anthony F. Aveni, ed. The Sky in Mayan Literature. Oxford, 1992.

4. Harvey M. Bricker and Victoria Bricker, "Classic Maya Prediction of Solar Eclipses". Current Anthropology, 24(1), 1983.

5. Victoria Bricker and Harvey M. Bricker,  "Zodiacal References in the Maya Codices", in Anthony F. Aveni, ed. The Sky in Mayan Literature. Oxford, 1992.

6. David Carrasco, Religions of Mesoamerica. Harper & Row, 1990.

7. Michael P. Closs. "Cognative Aspects of Ancient Maya Eclipse Theory", in Anthony F. Aveni, World Archaeoastronomy. Cambridge, 1989. "

8. Some Parallels in the Astronomical Events Recorded in the Maya Codices and Inscriptions", in Anthony F. Aveni, ed. The Sky in Mayan Literature. Oxford, 1992.

9. David Dearborn, "To the Limits: A  note on lunar precession in Mesoamerican astronomy",  Archaeoastronomy & Ethnoastronomy News, Number 3 March Equinox 1992. on-line

10. Munro S. Edmonston. The Ancient Future of the Itza: The Book of Chilam Balam of Tizimin. U of Texas, 1982.

11. Charles A. Hofling and Thomas O'Neil, "Eclipse Cycles in the Moon Goddess Almanacs in the Dresden Codex". The Sky in Mayan Literature. ed. Anthony Aveni. Oxford U, 1992.

12. John S. Justeson,  "Ancient Maya ethnoastronomy: an overview of hieroglyphic sources" in World  archaeoastronomy: Selected papers from the 2nd Oxford International Conference on Archaeoastronomy. A.Aveni, ed., Cambridge, Cambridge University Press, 1989.

13. Friar Diego de Landa,  Yucatan Before and After the Conquest (1566). Dover reprint of Gates' translation, 1978

14. Floyd G. Lounsbury. "Maya Numeration, Computation, and Calendrical Astronomy", in C.C. Gillispie, Dictionary of Scientific Biography, Vol. 15. Charles Scribner's Sons, 1978.

15. .............................. "A Derivation of the Mayan-to-Julian Calendar Correlation from the Dresden Codex Venus Chronology", in Anthony F. Aveni, ed. The Sky in Mayan Literature. Oxford, 1992.

16. M. W. Makemson. Astronomical Tables of the Maya. Carnegie Institute Publication 546, 1943.

17. Nancy K. Owen. "The use of eclipse data to determine the Maya correlation number", in A. Aveni, Archaeoastronomy in Pre-Columbian America. University of Texas, 1975.

18. Meredith Paxton.  "Codex Dresden: Late Postclassic Ceramic Depictions and the Problems of Provenience", in Merle Greene Robertson, ed., Sixth Palenque Round Table. Univ. of Oklahoma, 1986.

19. Ralph L. Roys (transl.), The Book of Chilam Balam of Chumayel (U. of Oklahoma Press, 1967). The quotation above is taken from the edition of the Book translated by Suzanne D. Fisher from Antonio Mediz Bolio's Spanish translation of the Yucatec text.

20. L. Satterthwaite, "Long Count Positions of Maya Dates in the Dresden Codex with Notes on Lunar Positions and the Correlation Problem". Proc. 35th Int. Cong. Amer. Mexico, 1962.

21. H. J. Spinden. "The Eclipse Tables of the Dresden Codex". Proc. 23rd Int. Cong. Amer. New York, 1928.

22. Charles Smiley. "The solar eclipse warning table in the Dresden Codex", in A. Aveni, Archaeoastronomy in Pre-Columbian America. University of Texas, 1975.

23. “Solar Eclipse Intervals in the Dresden Codex”, Journal of the Royal Astronomical Society of Canada, 59 (1965) on-line

24. The Thix and the Fox, Mayan Solar Eclipse Intervals”, Journal of the Royal Astronomical Society of Canada, 67 (1973). on-line

25. Dennis Tedlock. "Myth, Math, and the Problem of Correlation in Mayan Books", in Anthony F. Aveni, ed. The Sky in Mayan Literature. Oxford, 1992

26. J. E. Teeple. Maya Astronomy. Carnagie Institution Publication 403, no. 2, 1930.

27. J. Eric Thompson, A Commentary on the Dresden Codex. American Philosophical Society, Memoir no. 93, 1972.

28. R.H. Van Gent, A Catalog of Eclipse Cycles on-line

29. Felix Verbelen,  Eclipses and supernova 1054 in the Dresden Codex - A new astronomical approach online  (pdf file)

30. Catalogues of Solar and Lunar Eclipses on line

31. Carlos Villacorta and J.Antonio Villacorta, Codices Mayas, Guatemala, 1930. (The reproduction of the Dresden Codex has been seperately republished by Aegean Park Press).

32. R. W. Willson. Astronomical Notes on the Maya Codices. Papers Peabody Museum, Vol. 6, no. 3, 1924.