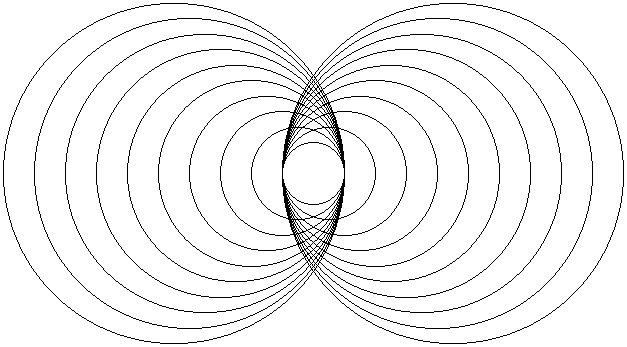
VESICA DERIVATIVES

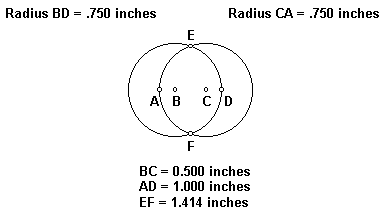
The radius of the circles below is .750 inches and the centers of the two circles are .5 inches apart (BC). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (AD). The distance between the two points where the circles intersect is 1.414 inches (EF). 1.414 is the square root of two.

This figure, demonstrating a ratio of 1.414 to one between the major axis (EF) and the minor axis (AD), may be constructed by dividing a segment in half and then dividing each of these segments in half, resulting in a segment divided into four equal quarters. Center the first circle on the inside point of the first segment (B) with a radius to the outside point of the fourth segment (D). Center the second circle on the inside point of the fourth segment (C) with a radius to the outside point of the first segment (A).

---

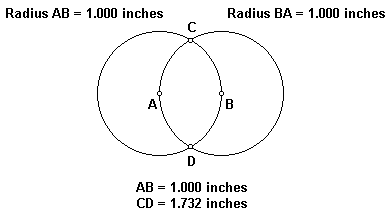
The Vesica Pisces is diagramed below. The radius of the circles are1.000 inches and the centers of the circles are 1.000 inches apart. The distance between the two points where the circles intersect (CD) is 1.732 inches. 1.732 is the square root of three.

---

---

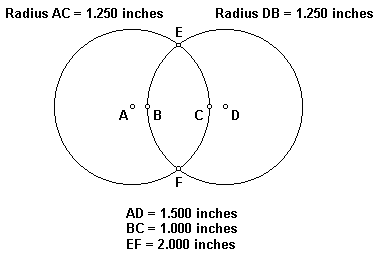
The radius of the circles below is 1.5 inches and the centers of the circles are 2 inches apart (AD). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (BC). The distance between the two points where the circles intersect is 2.236 inches (EF). 2.236 is the square root of 5.

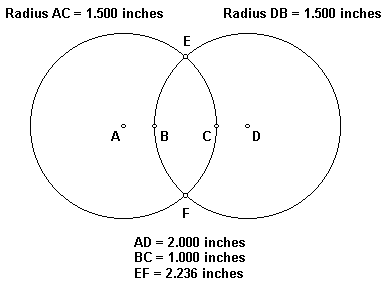
This figure, demonstrating a ratio of 2.236 to one between the major axis (EF) and the minor axis (BC), may be constructed by dividing a segment in half and then dividing each of these segments in half, resulting in a segment divided into four equal quarters. Center the first circle on the outside point of the first segment (A) with a radius to the inside point of the fourth segment (C). Center the second circle on the outside point of the fourth segment (D) with a radius to the inside point of the first segment (B).

---

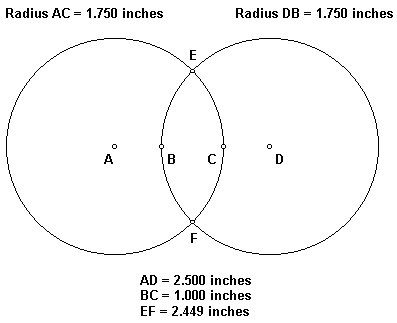
The radius of the circles below is 1.750 inches and the centers of the circles are 2.5 inches apart (AD). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (BC). The distance between the two points where the circles intersect is 2.449 inches (EF). 2.449 is the square root of 6.

---

---

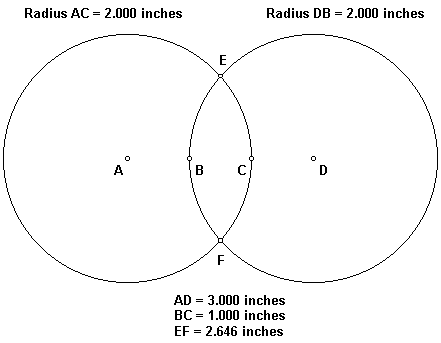
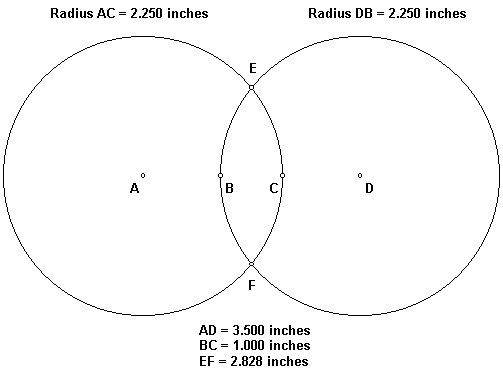
The radius of the circles below is 2.250 inches and the centers of the circles are 3.5 inches apart (AD). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (BC). The distance between the two points where the circles intersect is 2.828 inches (EF). 2.828 is the square root of 8.

Note: This image and the last image in the series are shown at one-half size.

---

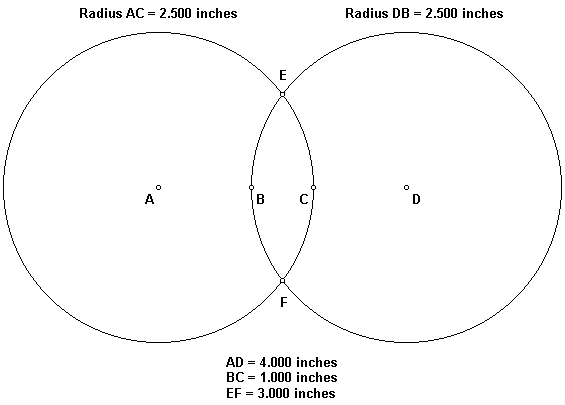
The radius of the circles below is 2.5 inches and the centers of the circles are 4 inches apart (AD). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (BC). The distance between the two points where the circles intersect is 3 inches (EF). 3 is the square root of 9.

---

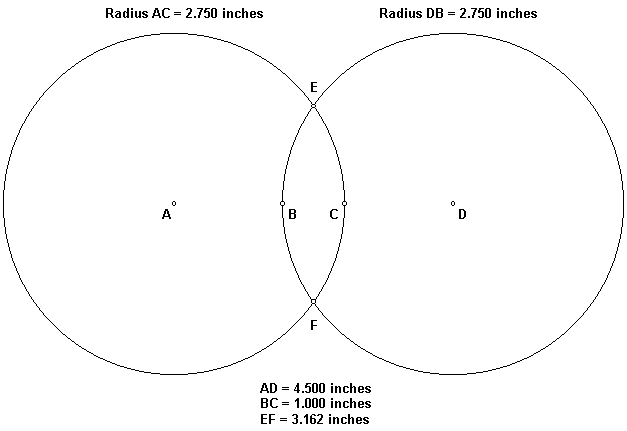
The radius of the circles below is 2.750 inches and the centers of the circles are 4.5 inches apart (AD). As a result, the distance between the two inner points of the circles at the middle height of the diagram is 1.000 inches (BC). The distance between the two points where the circles intersect is 3.162 inches (EF). 3.162 is the square root of 10.

---

Note: All of the figures in the series above may be constructed by dividing a 4.5 inch line into quarter inch segments and placing the centers and edges of the circles at the appropriate points. Square roots of higher integers may be demonstrated by adding quarter inch segments at both ends of the line and placing the centers and edges of the circles at the appropriate points.

The figures above geometrically demonstrate square roots with two intersecting circles as shown in the following table:

	Radius of circles	Distance between centers	Diameter plus distance between centers
√1 = 1	.500	0.0	1.0 + 0.0 = 1
√2 = 1.414	.750	.50	1.5 + .50 = 2
√3 = 1.732	1.00	1.0	2.0 + 1.0 = 3
√4 = 2	1.25	1.5	2.5 + 1.5 = 4
√5 = 2.236	1.50	2.0	3.0 + 2.0 = 5
√6 = 2.449	1.75	2.5	3.5 + 2.5 = 6
√7 = 2,646	2.00	3.0	4.0 + 3.0 = 7
√8 = 2.828	2.25	3.5	4.5 + 3.5 = 8
√9 = 3	2.50	4.0	5.0 + 4.0 = 9
√10 = 3.16	2.75	4.5	5.5 + 4.5 = 10

The diagram below is an overlay of all of the diagrams above. The diameter of the circle in the middle is one inch, giving a minor axis of one inch and a major axis of one inch, which is also the square root of one.