JUST INTONATION AND THE 25/24 INTERVAL
Mathematics, astronomy, geometry, geography, art, music and religion were all integrated in ancient times. Numerous surviving examples suggest that ancient Egyptian art was based on a strict canon that was followed for over 3,000 years. According to Plato, this was also true of ancient Egyptian music.
Tone is based on the frequency of sound waves. In modern western music, the note "A" in the middle octave has a frequency of 440 waves per second. This is the base frequency that is generally used to tune instruments. This is the same as the number of cubits in the baselength of the great pyramid. Doubling the frequency of a note produces the same note, one octave higher. Thus a frequency of 880 also produces an "A", as does a frequency of 220. An octave is comprised of all of the notes between the base note and it's double. The reason it is called an octave is because there are seven major notes in each octave, plus the double of the base note (A B C D E F G A).
Michael Hayes described a correlation between the 22/7 π ratio and the octave, with seven major notes and 22 notes in three full octaves (A B C D E F G A B C D E F G A B C D E F G A). There are actually only six full tones in an octave (not counting the double that starts the next octave). The reason there are seven major notes is because two of them are semitones. Five tones plus two semitones equals six. There are twelve semitones in an octave. The standard tuning of the 12 semitones is as follows:
| 440.00 = A |
| 466.16 = Bb |
| 493.88 = B |
| 523.25 = C |
| 554.36 = C# |
| 587.32 = D |
| 622.25 = Eb |
| 659.25 = E |
| 698.46 = F |
| 739.99 = F# |
| 783.99 = G |
| 830.60 = Ab |
| 880.00 = A |
The next higher octave may be calculated by doubling the frequency of each note and the next lower octave may be calculated by halving the frequency of each note. The seven major notes in each octave corresponds with the seven palms in a royal cubit. The six full tones in each octave corresponds with the ancient base six systems of mathematics.
The frequency chart above is based on the modern system of equal temperament tuning. Each of the 12 semitones are increased by a factor of the 12th root of 2, resulting in a doubling after the 12 semitones. The 12th root of 2 is 1.059463, so 440 x 1.059463 = 466.16, etc. Since the ratio between each semitone is 1.059463/1, the actual difference in wavelengths increases as the semitones go higher, even though the ratio between each semitone is the same. Using equal temperament tuning the semitone in the middle of the octave (Eb) is equal to the base note times the square root of two (622.25), the same as the number of cubits in the diagonal of the baselength of the great pyramid.
A string tuned to a base frequency of 440 waves per second (440 Hz) will also produce higher tones known as partials or harmonics. At the same time that the whole string vibrates at a frequency of 440 Hz, the string will also generate a vibration at twice the base frequency (880 Hz). This the second harmonic. The string's vibration at three times the base frequency is the third harmonic, etc. The volume of the harmonics is lower than the volume of the base frequency and the volume goes down as the harmonics go up.

When the same note is played by two different instruments at the same time, the frequency of both notes is the same, so every wave of both notes aligns, resulting in optimal consonance. When a note is played along with the same note one octave higher (the second harmonic), this is also very consonant because every other wave of the higher frequency aligns with every wave of the lower frequency.
What Pythagoras described as perfect fifths and perfect fourths are notes with low integer ratios in relation to the base note, also resulting in consonant sound. The third harmonic is three times the frequency of the base frequency (1320 Hz), taking it beyond the octave of the base frequency. This tone is brought back into the octave of the base frequency by dividing it by two (reducing it to it's next lower octave) resulting in a frequency of 660 Hz (440 x 3/2 = 660). This is called the perfect fifth because the 3/2 ratio occurs in the fifth note following the base note (from A to E). All of the semitones have fifths with a frequency ratio of 3/2, such as C to G, etc. The fifth is consonant because every third wave of the fifth aligns with every second wave of the base frequency.
The fourth harmonic is four times the frequency of the base frequency (1760 Hz). This tone is brought back into the octave of the base frequency by dividing it by three, resulting in a frequency of 586.66 Hz (440 x 4/3 = 586.66). This is called the perfect fourth because the 4/3 ratio occurs in the fourth note following the base note (from A to D). All of the semitones have fourths with a frequency ratio of 4/3, such as C to F, etc. The fourth is consonant because every fourth wave aligns with every third wave of the base frequency. Khafre's pyramid also expresses perfect fifths (baselength over height = 3/2) and perfect fourths (height over half-base = 4/3).
Claudius Ptolomy directed the library at Alexandria in the first century A.D. He described a system of music known as Just Intonation. In this system, the ratio between the flats and sharps of all of the notes is the precise fraction of 25/24 (ie: the ratio between 5/4 (E) and 6/5 (Eb) is 25/24). Ptolemy's system is distinguished from the Pythagorean system in that Pythagoras believed that the ratios of all of the notes had to be multiples or powers of either 2 or 3, with no higher prime number allowed. Thus, the Pythagorean system is also referred to as a three limit system. Ptolemy's system allows ratios with multiples and powers of 2, 3 or 5, thus it is also known as a five limit system.
Since Pythagorean intonation only uses multiples of 2 and 3, the Pythagorean scale is generated by multiplying the base frequency by perfect fifths (3/2) and perfect fourths (4/3). The first multiplication results in the perfect fifth of 3/2. The second multiplication is 3/2 x 3/2 = 9/4, which is outside the octave, so it is divided by two to give 9/8. The third multiplication is 9/8 x 3/2 = 27/16. To the left side, the base frequency is repeatedly multiplied by perfect fourths. Here is the Pythagorean scale:
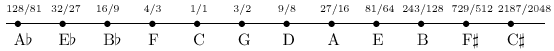
This is known as the Pythagorean cycle of fifths. The twelth multiplication gives a G# that is virtually the same ratio as Ab. Thus, the Pythagorean scale is comprised of 12 semitones and this is one of the reasons modern western scales have 12 semitones. The five limit system of Ptolemy is not limited to 12 tones.
Even though all of the ratios in the Pythagorean scale are based on multiples and powers of 3 and 2, some of the ratios are so complex that they are not nearly as consonant as the lower ratios available in the five limit system of Ptolemy. The five limit system also allows for pure tones based on the fifth harmonic, which Pythagorean intonation does not. The five limit system includes pure harmonic thirds (5/4), sixths (5/3), minor thirds (6/5) and minor sevenths (9/5) that are not available in the three limit system. Modern western music does not use the three limit or the five limit system.. With intervals based on the 12th root of two, none of the ratios between the tones in equal temperament are perfect harmonic ratios.
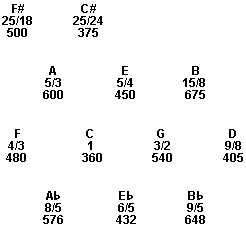
The perfect fifth of 3/2 and the perfect fourth of 4/3 that are present in both 3 limit and 5 limit systems are reciprical ratios in the sense that 1 x 3/2 x 4/3 = 2. The five limit system allows for a scale where all of the tones are reciprical. The chart below shows the recipricals on the left side, all of the 25/24 ratios in brackets on the right side and the frequencies on the far right, based on an octave from C - 360 to C - 720:
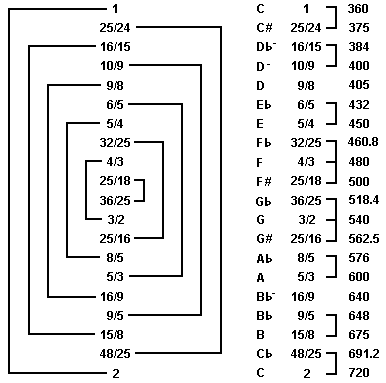
As shown in the cycle of fifths diagram, the Pythagorean system is one dimensional. Ptolemy's five limit system can be diagramed two dimensionally. The diagram below shows the notes listed in the chart above.
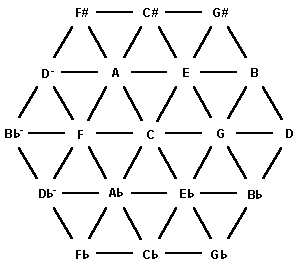
The diagram below shows the same notes by their ratios. All of the notes connected by horizontal lines are in the ratio of 3/2 from left to right (or 3/2 divided by 2, when necessary to bring the fraction on the right back into the octave). All of the notes connected by lines going up and to the right are in the ratio of 5/4 (or 5/4 divided by 2) and all of the notes connected by lines going down and to the right are in the ratio of 6/5 (or 6/5 divided by 2).

The mathmatician and music theorist Leonhard Euler suggested that ideally the frequencies of all of the notes should be whole numbers. The philosopher and music theorist Jean Jacques Rouseau suggested the 12 tone monochord below, applying 5 limit ratios to the Pythagorean scale. Using C 360 as the base frequency, this scale meets Euler's requirement that the frequencies of all of the notes are whole numbers. Just as in the 19 tone scale above, the ratio between the sharps and flats of all of the notes is the precise fraction of 25/24: