|
"We cannot impose our wills on nature unless we first ascertain what
her will is. Working without regard to law brings nothing but
failure; working with law enables us to do what seemed at first
impossible."
- Ralph Tyler Flewelling
3. Nature's Mysterious
One evening in 1940 I gave a talk, illustrated with slides, to the
New York chapter of the American Statistical Association.
After the
meeting I happened to overhear one professor say to another,
"I
never saw so many coincidences- in my life!"
What that scholarly gentleman meant, of course, was that the cycles
I had illustrated and discussed were nothing but coincidences.
I
might have agreed with him about any one cycle, but I had faith that
all of them could not possibly be coincidences. At that time,
however, this was merely faith on my part, and I knew it. That faith
has been strong enough to nourish me for more than three decades,
and it has grown stronger with the years as I have watched
"coincidence" piled on "coincidence," as the pieces began to fit
together, and as the clues to the mystery were uncovered in mounting
numbers. Faith is now being justified by indisputable fact.
I have never been one to go off the deep end by confusing thinking
and feeling with knowing.
"It looks as if there is something here,"
I would say to myself as I studied a series of figures, "but of
course it may be nothing but chance, nothing but coincidence." (In
the early days we did not know how to determine, mathematically, the
number of times out of 100, or 1,000, or 10,000 that any particular
cycle could come about by chance.)
How can one tell, in any given instance, whether or not a regular
rhythm that one discovers is caused by a real underlying force or
merely by chance?
Let's begin with some common sense and simple
logic. If a cycle has repeated enough times, with enough regularity
and with enough strength, the chances are that it is significant.
Such regularity cannot reasonably be mere accident.
Pick up a pack of playing cards and begin to deal, face up. The
first card is red, the second black, the third red, and the fourth
black. You now have two waves of a regular cycle - red, black, red,
black. This could easily happen by chance.
You continue to deal. Red, black, red, black. Four times in a row
now. This regular alternation could still be chance, but it couldn't
be chance if it were to continue much longer.
Resume dealing. Red, black, red, black, red, black. Seven times now!
It could still be chance but it is less and less likely. It begins
to look as if somebody has stacked the cards. You go through the
entire deck. Twenty-six times of alternating red and black cards!
"Somebody certainly stacked this deck," you exclaim. "It couldn't
happen this way by chance once in a million times."
You underestimate!
The mathematical odds that black and red cards
would alternate in twenty-six waves, accidentally, are one in a
quadrillion! In this chapter you will be introduced to cycles that
have repeated at least twenty-six times over a period of more than
two hundred years.
Later on you will meet cycles that have repeated
more than one hundred times - back to the year 600 B.C.!
Will Nature's Clues Solve Our Mystery?
In the past thirty years a considerable amount of our research at
the Foundation has involved cycles in the natural sciences, for
three important reasons.
-
First, rhythmic cycles are almost universal
in nature.
-
Second, natural-science cycles are usually much less
complicated than human cycles and thus easier to study.
-
Third, when
the wavelengths of natural-science cycles are the same as
wavelengths of cycles in the social sciences we have reason to
believe that we are approaching the very heart of our mystery.
Unless you have studied the subject, you would be amazed at the
universality of rhythmic cycles in nature.
The abundance of birds,
fish, insects, reptiles, microorganisms, and mammals fluctuates in
rhythm. Tree rings, evidence of annual growth, are wide and narrow
in rhythmic cycles. Water levels in our rivers and lakes go up and
down in cycles. Earthquakes recur at rhythmic intervals. So do
volcanic eruptions. Sedimentary rock deposits are first thick and
then thin in layers that evidence rhythm.
All aspects of weather
show rhythmic cycles - although very complicated ones - and, of course,
many stars pulsate rhythmically.
Thus we study rhythms wherever they can be found, not because we
have any special interest in ornithology, herpetology, ichthyology,
or geology, but because the cycles in these and other branches of
natural science are often identical with the cycles of man. Because
they are identical they may have a common cause.
For example, there is nothing very remarkable in the fact that there
is a similar eight-year cycle in stock prices and in manufacturing
production. You might expect that the one would go up and down with
the other. However, if the weather and earthquakes and sunspot
eruptions also have eight-year coincident cycles, you are confronted
with a situation that makes you feel you are on to something big.
Studying nature's behavior, then, may teach us more about man's
behavior. So, like Alice in Through the Looking Glass, we will
momentarily turn our back on what we wish to know so that we will
know it better.
We will face in the other direction, away from the
social sciences, and review a few mysterious cycles in wildlife,
something that the United States Army Air Force, to their regret,
once neglected to do in the early months of World War II.
The Battle of Ascension Island
Ascension Island is little more than a few square miles of volcanic
matter situated in the Atlantic Ocean halfway between South America
and Africa. It was selected in 1942 as an ideal spot for the Army
Air Force to build a stopover landing field for their short-range
medium bombers, which were unable to cross the ocean nonstop.
Hurriedly they built their field, and the B-25's and the B-26's
began their endless procession across the Atlantic. Ascension
Island, however, is accustomed to another type of winged visitor,
for it is the nesting ground of the sooty tern, a bird with a unique
breeding cycle. It returns to its favorite breeding ground every 9.7
months to hatch its oversized eggs!
But the Air Force was not aware of this rhythm of nature, and soon
after the landing strip was completed, thousands upon thousands of
terns began swarming over the field, which, unfortunately, had been
built in the middle of a nesting area.
The small web-footed creatures were more than a nuisance; they were
a frightening hazard to the fliers. Whenever a plane took off or
landed, the startled terns would leave the ground and fill the sky
with tens of thousands of pounds of flying gull meat only slightly
less dangerous than antiaircraft shells. Although the Air Force, in
order to save lives and planes, might have been tempted to consider
"genocide" on the sooty terns, they could not, for they had promised
to respect the flora and fauna of the island.
To help resolve the dilemma Dr. James P. Chapin, an ornithologist
with the American Museum of Natural History, was consulted.
Eventually he collected sufficient data to compute that terns
returned to nest every 9.7 months on the average. After discarding
several ideas to force the birds to move away, he finally hit upon
the simple process of breaking their eggs.
He had learned that the
parent bird rarely returned to the scene of a nesting that had ended
in disaster. By forcing the adult birds to move elsewhere, he not
only saved them as future breeding stock, but undoubtedly saved the
lives of many young pilots.
What brings the sooty tern back in a 9.7-month cycle? In more
temperate climates of the world, which have wide variations of
climate, temperature, and weather conditions, birds have an annual
breeding cycle. But Ascension Island is near the equator. There is
no distinct change in the weather from season to season, nor is
there any variation in the amount of daylight.
Yet every 9.7 months
a million or more terns arrive at Ascension to hatch their young.
The Odd-Year Bird
A small North American bird with the unlikely name of evening
grosbeak is another winged creature with a baffling cycle.
It
migrates into New England in large numbers - but only in the
odd-numbered years. Only three times since 1913 have the grosbeaks
deviated from their strange timetable. They were due in 1915 but
failed to show, coming instead a year later. In 1917 they returned
to schedule, but came again in 1918 also. In 1937 they never
bothered to show up at all.
Except in these years they have made
their appearance every odd-numbered year with dramatic regularity.
That the grosbeak's regularity was not perfect, over the years,
demonstrates an important characteristic of many cycles: after an
interruption they tend to return to their old rhythm. In 1937, when
it was due, the grosbeak did not appear, but it did not come the
next year either. It waited until its next "due" year, 1939, to
return.
The reason for this invasion of New England in an almost
perfectly regular two-year cycle is not yet known.
The Stay-at-Home Bird
Nearly all bird populations fluctuate in cycles.
Studies by J.
Murray Speirs of the Research Council of Ontario concentrated on
birds that frequent the Toronto region. He discovered that the
northern shrike, the rough-legged hawk, and the snowy owl have
populations that fluctuate in cycles of three to five years. The
pine grosbeak has a five-to-six-year cycle, and the horned owl has a
cycle of nine to eleven years.
Dr. Leonard W. Wing, through another study, concluded that the hairy
woodpecker, the downy woodpecker, and the bobwhite have an abundance
cycle of 50.7 months. Changes in bird abundance are usually
associated with their migrations. Many experts feel that food
scarcity, which seems to occur at cyclic intervals, forces birds to
move toward strange but warmer country.
Eventually, when their
search is rewarded with a surplus of food, their fertility
increases, they multiply, and they spread out over larger land
areas.
But the bobwhite's activities almost destroy this explanation, for
few of these small reddish-brown birds ever die more than a mile
from the nest where they were hatched. Migration cannot possibly
affect their population fluctuations, and yet they have a definite
cycle of 50.7 months. Whatever force causes this cycle does so in
their own neighborhood.
And this force is not yet known.
The Rise and Fall of the Lynx
The Canadian lynx is another prime example of one of the most
baffling aspects of animal life - its rise and fall in population... the cycle of abundance.
Patrolling the northernmost regions of
Canada in search of his favorite food, the snowshoe rabbit, the lynx
moves with huge running strides on padded feet large enough to
prevent him from sinking into the soft snow. But while he is a
hunter, he is also the hunted, for his skin is instantly convertible
to cash at the nearest trading post.
Unless we are trappers, hunters, or fishermen, we normally think of
animal populations as relatively stable, a notion that is far from
actuality.
Animal populations vary tremendously from year to year,
even from month to month. Since the lynx is a favorite of
north-country trappers, year-by-year records of its population are
available over a long period of time, and it thus makes excellent
study material.
Of course, there are no actual lynx censuses, but there are records
of the offerings of lynx skins by trappers, particularly to the
Hudson's Bay Company. As the efforts of trappers to earn a
livelihood are fairly constant, biologists feel that the records of
skin offerings constitute a reasonably reliable index of the
abundance of the animal in its wild state.
Now I ask you to look at an almost unbelievable "picture" of a cycle
(see Figure 2).
Note that this 9.6-year cycle in Canadian lynx
abundance has been repeating itself in almost perfect rhythm since
1735.
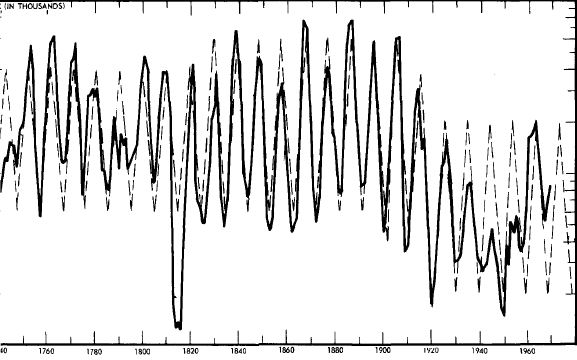
Fig. 2.
The 9.6-Year Cycle in Lynx Abundance, 1735-1969
Note: To help you visualize the regularity of the cycle under
discussion
a broken zigzag line diagramming a perfectly regular
cycle of the same length
will be included in all cycle charts.
Except for the fact that during the last fifty to sixty years the
catch has been considerably lower, the most notable features of this
record are the tremendous fluctuations that characterize these
figures and the amazing regularity of the fluctuations.
The graph
shows a range from under 2,000 skins in a poor year to over 70,000
in a good one. Intervals between one high and the next, or one low
and the next, normally vary from eight to ten years. Over the span
of the record they average precisely 9.6 years.
Because of the wide fluctuation in skins from a high year to a low,
and because of its regularity, the Canadian lynx cycle has received
wide attention. Although there is general agreement that it has not
continued to fluctuate in such a regular rhythm for over two hundred
years purely by chance, there is little agreement as to the cause.
One attempted explanation is based on a similar cycle in the rise
and fall of abundance of snowshoe rabbits, the most important
item of food in the lynx diet. But this raises an obvious and
unanswered question. What causes the 9.6-year cycle in the snow-shoe
rabbit?
The 9.6-year cycle in population is characteristic of much wildlife.
The coyote, red fox, fisher, marten, wolf, mink, and skunk have
abundance cycles of the same period (average wavelength), all
reaching their highs and lows in abundance at about the same time on
the calendar.
In Illinois, and in much of the Midwest, a pesky white-winged insect
called the chinch bug also has a 9.6-year cycle, at the peak of
which up to 70 million have been known to cover one acre, wreaking
havoc on cereal crops.
Since it is rather difficult to imagine 70
million of anything, this reduces to 1,600 bugs per square foot!
Salmon, Lost and Found
Atlantic salmon fluctuate in abundance in a cycle whose period is
identical with the lynx in Canada and the chinch bug in Illinois
(see Figure 3).
The Restigouche Salmon Club is an ultra-exclusive group of sportsmen
who fish for salmon on the Restigouche, a river approximately 125
miles long flowing between the Gaspe Peninsula and New Brunswick and
emptying into the Gulf of St. Lawrence. Careful records kept by its
members of the catch of salmon per rod per day indicate that the
abundance of salmon fluctuated in a 9.6-year cycle from 1880 to
1930.
More recent figures supplied to me by the club's president
pick up the identical rhythm, which is in step with the previous
cycle. This is an important piece of evidence, indicating that here
is a cycle that cannot possibly be ascribed to chance. I will
elaborate on the significance of this in a later chapter.
In another 1960 study, traces of the same 9.6-year cycle in Atlantic
salmon were discovered thousands of miles away in Wye, England.
The practical use to which cycle knowledge can be put is obvious in
our brief look at salmon abundance, for the problem of occasional
scarcity in this popular seafood is of vital importance to the
European fishing industry.
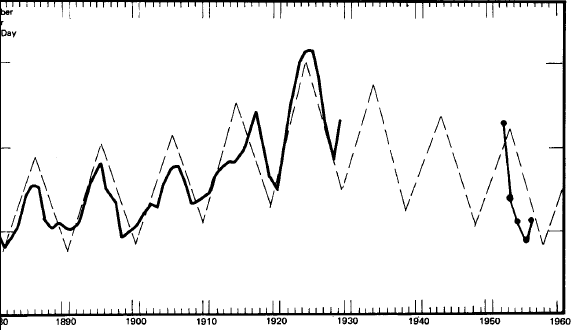
Fig. 3.
The 9.6-Year Cycle in Atlantic Salmon Abundance, 1880-1956
Restigouche Salmon Club catch per rod per day, smoothed, 1880-1929;
values 1952-1956 actual. No other values available.
To be able to predict the good and
bad years for salmon fishing can save thousands of man-hours and
millions of dollars. We need not wait until we solve our mystery to
take advantage of knowledge we already possess.
The Rodent Who Dies in a Cycle
The Norwegian word for "destroying" is lemmus, or lemming.
On the
average of every 3.86 years a six-inch rodent by the same name
sweeps down from the hills of Norway in hordes, destroys everything
in its path, and continues on until it reaches the sea. But it
doesn't stop at the water's edge. It continues on, destroying itself
by drowning. A few, who for some inexplicable reason remain behind,
become the nucleus for the new horde that will migrate toward the
sea, on the average, 3.86 years later.
The cause
of the lemming's rush to death on such a regular schedule is not
known.
Norway also has a 3.86-year cycle in the abundance of foxes, and in
the United States the growth of limber pine seems to have an
identical cycle length. What obscure force could possibly affect the
growth of certain trees in America and also influence the lemmings
and foxes of Norway?
Trees, Prices, and Electricity
In the last paragraph I mentioned tree growth.
Measuring this growth
is accomplished simply by measuring the varying widths of tree
rings. Trees grow by adding layers of wood. Winter growth is hard
and compact. Summer growth is soft and porous. Cut down a tree and
you can measure its rings for the growth of any particular year.
When the tree has had a good year of growth, the layers for that
year are thick; when growing conditions are poor, the layers are
thin.
There is a tendency for several pairs of thick layers to be
followed by several pairs of thin layers. When this alternation is
regular, we have rhythmic cycles in the tree-ring widths.
Arizona trees and their rings have been the subject of study for
many years. One study, which traced the growth of trees back to the
ninth century, indicates a fifty-four-year cycle. In England, coal,
pig-iron, and lead production have the same cycle length. France has
a fifty-four-year cycle in imports and exports and total foreign
trade.
In 1922 Lord Beveridge noted a fifty-four-year cycle in wheat
prices, and the United States is now old enough to have experienced
three such cycles in average wholesale prices. Coincidences?
Other cycles of a shorter length have also been discovered in tree
rings, and one in Arizona of 16⅔ years has also been discovered in
the trees on Java.
A third tree-ring cycle, forty-two years in length, is of interest
because it has characteristics that we find in many of our cycle
studies. Its forty-two-year cycle repeats for perhaps ten regular
waves and then we will have only one high in the next eighty years
or so. Then we might have two waves where there should be three.
Finally it resumes its old and regular forty-two-year rhythm as if
the force that caused the forty-two-year cycle always existed but
was diverted, for a time, either according to chance or to some law
not yet understood.
Trees have another fascinating cycle. Their electric potential, or
voltage, goes up and down in rhythm. If you drill two small holes
vertically, a yard or so apart, in the trunk of a living tree and
insert one end of a piece of wire into each hole, an electric
current will flow along the wire, as if the tree were an electric
battery. With a battery, however, the voltage is constant. In a tree
the voltage varies.
Also, the current from a battery always flows
one way, but the current from a tree sometimes flows one way and
sometimes the other.
Dr. H.S. Burr, of Yale University, has kept constant records of
changes in voltage for a number of trees in the New Haven area, day
and night, for many years. His records disclose two startling facts.
First, the voltage in trees goes up and down in a cycle of
approximately six months. Second, another tree of the same kind,
even thirty miles away, behaves in the same manner. When the current
flows up in one tree, it does the same in the other. When it flows
down in one, it does likewise in the other.
Dr. Burr attempted to
link this change in voltage to possible similar changes in the
barometric pressure, temperature, or humidity in the area, but
eventually he abandoned all of these as the possible cause for the
trees' strange behavior.
Let us examine this "clue" for a moment. What could possibly cause
trees to act this way? Obviously the cause must be environmental.
Something unknown in the air or in the earth must influence their
behavior. But what? Since we see the effects we know there must be a
cause. Something does exist to make trees act this way and this
"something" has force, a force that repeats in a cycle. What is this
force?
The Clearinghouse
In their search to understand nature several generations of
scientists have noted the existence of rhythmic behavior.
Working in
their own field of interest, they often observed and commented on
what seemed to be patterns and sub-patterns in events. But prior to
the creation of the Foundation for the Study of Cycles there was no
clearinghouse that could gather information about cycles in
meteorology, let us say, and pass this on to those doing research
with cycles in economics, medicine, agriculture, or sociology.
Some
scientists, even today, are not aware of cycles in any field but
their own.
Yet if cycles are truly characteristic of all living things, is it
not logical that a knowledge of cycles, in animal abundance, for
example, might provide the geologist or the meteorologist with
information that could reinforce his own discoveries? Without this
valuable interchange of cycle information between the various
branches of science, will these dedicated people ever truly
understand their own particular science?
Although your only interest in bugs may be to destroy those who feed
on your rose bushes, let's assume for the moment that you are an
entomologist and your life's work has been the study of the
grasshopper. Because of your research you are aware that crop losses
and pest-control expenses caused by these insects deprive farmers of
millions of dollars each year.
However, your studies have been long and thorough and you are aware
of the fact that the population of grasshoppers fluctuates in cycles
and hence is partially predictable. You know that there are at least
three cycles in the abundance of grasshoppers, one with a period of
9.2 years, one with a period of 15 years, and one with a period of
22.7 years. It is as if several forces were influencing their
abundance simultaneously.
Now, of course, all three of these cycles are meaningful in your
work but you are particularly interested in the 9.2-year cycle
because it is the shortest one, and thus repeats most often. One day
you happen upon some of the material published by the Foundation for
the Study of Cycles, and what you read dumbfounds you, for you learn
that the same 9.2-year cycle exists in many other phenomena.
There
are cycles of similar length in the water level of Lake Michigan, in
the alternate thickness of tree rings, in business failures, and in
prices.
A 9.2-year cycle has been continuously present in pig-iron
and copper prices since 1784; a 9.2 year cycle has been evident in
industrial-stock prices since their beginning in 1871, in
railroad-stock prices since their beginning in 1831. Partridge
abundance in Hertfordshire, England, shows a cycle of approximately
9.2 years, and tree rings at Santa Catalina, Arizona, tend to be
thicker at 9.2-year intervals.
Later you discover other "coincidences." From an old issue of
Cycles, the Foundation's monthly magazine, you learn that the
Smithsonian Institution has published a paper by Dr. C.G. Abbot,
based on forty years of observations, that states that radiation of
heat from the sun varies in cycles of approximately 22.7 years, the
same length as your longest grasshopper cycle.
Also, in the same
issue, you encounter your long cycle again at, of all places, an old
Bohemian estate in Krumau, Czechoslovakia. Data on the annual bag of
partridge from this estate covering a period from 1727 to 1909 show
highs and lows at 22.7-year intervals.
The odds are great that your work in entomology will never be quite
the same again.
You will realize for the first time that the cycles
you are dealing with in grasshoppers may be part of something much
larger, and of fundamental importance to the world.
The Lowest Form of Life
No book that you can comfortably hold could catalogue all the known
cycles in natural science.
There are endless numbers of rhythms,
some lesser known, such as the cyclic hatching of many insects,
cyclic pigment changes, cyclic metabolic rates, cyclic chemical
changes of the body - even cyclic variation of milk produced by cows.
There is also the rhythm of feeding patterns of many animals,
including bedbugs, chipmunks, rabbits, and lizards.
Even the amount of pollen gathered by bees fluctuates in a cycle.
Unlike Noah, I have made no attempt to include every species in my
"ark," for it would sink from sheer weight and you would eventually
cease reading from boredom. The purpose of this chapter has been
accomplished if you are now aware that there is rhythm in nature.
Later on you will meet many more cycles in nature as we compare them
to cycles in other sciences.
But before we leave the birds and the bees and the lynx and the
salmon there is one more cycle in nature that I cannot resist
introducing to you. Drifting in the oceans and many freshwater lakes
of the world are microscopic organisms called plankton. Although
plankton is one of the lowest forms of life, it is, nevertheless, an
important source of nourishment for most of the creatures that
inhabit the underwater world.
Lowly though it may be, it has one thing in common with the
grasshopper, the salmon, the partridge, the lynx, and even the tree.
It has a cycle of its own. In 1926 a study of plankton in Lake
Michigan was initiated by the Water Purification Division of Chicago
and by 1942 more than 12,000 samples had been taken from the lake.
The average annual total plankton yield suggested the occurrence of
a periodic four-year cycle in which two rather high production years
are followed by two rather low production years.
As with many of the tiny plankton's larger brothers and sisters in
the world of nature there is no logical or accepted explanation for
this cycle.
Back to Contents
|

