|

by Larry Bradley
2010
from
ChaosAndFractals-TheSpaceTelescopeScienceInstitute
Website
Weather prediction is an extremely difficult problem. Meteorologists
can predict the weather for short periods of time, a couple days at
most, but beyond that predictions are generally poor.
Edward Lorenz was a
mathematician and meteorologist at the Massachusetts Institute of
Technology who loved the study of weather. With the advent of
computers, Lorenz saw the chance to combine mathematics and
meteorology. He set out to construct a mathematical model of the
weather, namely a set of differential equations that represented
changes in temperature, pressure, wind velocity, etc.
In the end, Lorenz stripped the weather
down to a crude model containing a set of 12 differential equations.
On a particular day in the winter of 1961, Lorenz wanted to
re-examine a sequence of data coming from his model. Instead of
restarting the entire run, he decided to save time and restart the
run from somewhere in the middle. Using data printouts, he entered
the conditions at some point near the middle of the previous run,
and re-started the model calculation.
What he found was very unusual and
unexpected. The data from the second run should have exactly matched
the data from the first run. While they matched at first, the runs
eventually began to diverge dramatically - the second run losing all
resemblance to the first within a few "model" months.
A sample of the data from his two runs
in shown below:

Lorenz's Sample Data
At first Lorenz thought that a vacuum
tube had gone bad in his computer, a Royal McBee - an extremely slow
and crude machine by today's standards.
After discovering that there was no
malfunction, Lorenz finally found the source of the problem. To save
space, his printouts only showed three digits while the data in the
computer's memory contained six digits. Lorenz had entered the
rounded-off data from the printouts assuming that the difference was
inconsequential.
For example, even today temperature is
not routinely measured within one part in a thousand.
This led Lorenz to realize that long-term weather forecasting was
doomed. His simple model exhibits the phenomenon known as
"sensitive dependence on initial conditions."
This is sometimes referred to as
the butterfly effect, e.g. a
butterfly flapping its wings in South America can affect the weather
in Central Park. The question then arises,
Why does a set of completely
deterministic equations exhibit this behavior?
After all, scientists are often taught
that small initial perturbations lead to small changes in behavior.
This was clearly not the case in Lorenz's model of the weather.
The answer lies in the nature of the
equations; they were nonlinear equations.
While they are difficult to solve,
nonlinear systems are central
to
chaos theory and often exhibit
fantastically complex and chaotic behavior.
What is The Butterfly Effect?
from
WiseGeek Website
The butterfly effect is a term used in Chaos Theory to describe how
tiny variations can affect giant systems, and complex systems, like
weather patterns.
The term butterfly effect was applied in
Chaos Theory to suggest that the wing movements of a butterfly might
have significant repercussions on wind strength and movements
throughout the weather systems of the world, and theoretically,
could cause tornadoes halfway around the world.
What the butterfly effect seems to posit, is that the prediction of
the behavior of any large system is virtually impossible unless one
could account for all tiny factors, which might have a minute effect
on the system. Thus large systems like weather remain impossible to
predict because there are too many unknown variables to count.
The term "butterfly effect" is attributed to Edward Norton Lorenz,
a mathematician and meteorologist, who was one of the first
proponents of
Chaos Theory.
Though he had been working on the theory
for some ten years, with the principal question as to whether a
seagulls’ wing movements changes the weather, he changed to the more
poetic butterfly in 1973.
A speech he delivered was titled, “Does the Flap of a Butterfly’s
Wings in Brazil Set off a Tornado in Texas.” Actually, fellow
scientist, Philip Merilees created the title. Lorenz had
failed to provide a title for his speech.
The concept of small variations producing the butterfly effect
actually predates science and finds its home in science fiction.
Writers like Ray Bradbury were particularly interested in the types
of problems that might occur if one traveled back in time, trailing
anachronisms.
Could small actions taken in the past
dramatically affect the future?
Fictional treatments of the butterfly effect as applies to time
travel are numerous. Many cite the 2005 Butterfly Effect film
as a good example of the possible negative changes that small
behaviors in the past could have on the future, if one could
time travel.
Actually, a better and more critically
accepted treatment of this concept is the 2000 film Frequency.
In the film a father and son communicate over time through radio
waves and attempt to change the past for the good.
In human behavior, one can certainly see how small changes could
render behavior, or another complex system, extremely unpredictable.
Small actions or experiences stored in the unconscious mind, could
certainly affect a person’s behavior in unexpected ways.
One looks at teen suicide for example, where no instance of previous
depression has occurred. Loved ones are often left wondering what
the many small factors were that precipitated a suicide. Further,
people often agonize about the small details they did not see as
possible factors for an unexpected suicide.
However, there are plenty of ways that such a behavior would be
unanswerable according to the butterfly effect.
Minute actions and experiences dating
from childhood stored in the unconscious mind are not accessible
when a person has died, and they may be hard to access without
hypnosis or therapy when a person is living.
The "Butterfly Effect"
July 10, 2003
from
Templarser Website
The "Butterfly Effect" is the propensity
of a system to be sensitive to initial conditions.
Such systems over time become
unpredictable, this idea gave rise to the notion of a butterfly
flapping it's wings in one area of the world, causing a tornado or
some such weather event to occur in another remote area of the
world.
Comparing this effect to the domino effect, is slightly misleading.
There is dependence on the initial sensitivity, but whereas a simple
linear row of dominoes would cause one event to initiate another
similar one, the butterfly effect amplifies the condition upon each
iteration.
The butterfly effect has been most commonly associated with the
Weather system as this is where the Lorenz Attractor
discovery of "non-linear" phenomenon began when
Edward Lorenz
found anomalies in computer models of the weather.
But
Henri Poincaré had already made
inroads into this area.
Mapping the results in "phase space"
produced a two-lobe map called the Lorenz Attractor. The word
attractor meaning that events tended to be attracted towards
the two lobes, and events outside of the lobes are such things like
snow in the desert.
The attractor acts like an egg whisk, teasing apart parameters that
may initially be close together, this is why the weather is so hard
to predict.
Super computers run several models of
the weather in parallel to discover whether they stay close together
or diverge away from each other. Models that stay similar in nature
give an indication that the weather is relatively predictable, and
are used to indicate the confidence level that Meteorologists have
in a prediction.
It is not just the weather though that is subject to such phenomena.
Any "Newtonian Classical" system where
one system is in competition with another, such as the "Chaotic
Pendulum" which plays magnetism off against gravity will exhibit "sensitivity
to initial conditions".
Animal populations may also be subject
to the same phenomena.
Work done by
Robert May, suggests that
predator-prey systems have complex dynamics making them prone to
"boom" and "bust", due to the difference equations that model them.
Such a system even with two variables such as Rabbits and Foxes can
create a system that is much more complex than would be thought to
be the case.
Lack of Foxes means that the Rabbit
population can increase, but increasing numbers of Rabbits means
Foxes have more food and are likely to survive and reproduce, which
in turn decreases the number of Rabbits.
It is possible for such systems to find
a steady state or equilibrium, and even though species can become
extinct, there is a
tendency for populations to be robust,
but they can vary dramatically under certain circumstances. Real
populations of course, have more than two variables
making them ever more complex.
But as can be seen from the diagram,
such systems are not as simple as might be thought.
The chemical world is also not free from such intrusions of
non-linearity.
In certain cases chemical feedback
produces effects as that in the
Belousov-Zhabotinsky reaction,
creating concentric rings, which are produced by a chemical change,
whose decision to change from one state to another cannot be
predicted. The B-Z chemical system is currently being trialed as a
means to achieve artificially intelligent states in robots.
Phase space portraits of liquid flow show that they too are subject
to the same kind of non-linearity that is inherent in other physical
systems.
It may be apparent when turning on a tap
that sporadic drips become "laminar" as the flow increases. What
might not be apparent is the nature of the change from semi-random
to continuous. It may seem rather at odds with intuition that such
natural systems have inherent behavior that is not random, or indeed
that is not capable of being predicted. It may also seem that "not
random" means "predictable".
Natural systems can present a tangled mix of determinism and
randomness, or "order" and "chaos".
In such cases as water moving from drips
to continuous flow, pictures called "Bifurcation diagrams"
demonstrate the nature of movement from order into chaos. This
bifurcation is based on Robert May's work, but one of the intriguing
things about bifurcations is that the same pattern occurs no matter
what system is iterated.
In fact
Mitchell Feigenbaum discovered
that there was a "constant of doubling" hidden in amongst all these
systems.
Electronic apparatus is also not free from such effects, and it is
perhaps ironic, that we think of electronic apparatus as as being
the epitome of predictable determinism and ruthless clockwork
efficiency. Indeed the powerful computers used to predict weather,
would seem ineffectual if they were not ruthless automatons. But
such effects occur only in certain circumstances where there is
"sensitivity to initial conditions".
Amplifiers for instance, produce a howl
when feedback occurs as they go into a stable state of oscillation.
Logic gates as used in computers have to
select a "0" or a "1", and this relies on choosing between two
states whose boundary is indeterminate, and it is when a computer
confuses a "0" for a "1" or vice versa that mistakes occur.

Phase space
portrait of regular
flow in a Taylor-Couette system

Phase space
portrait of chaotic
flow as the attractor becomes "strange"
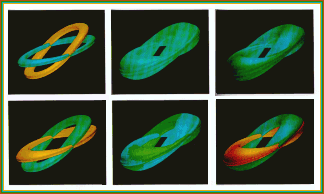
Phase space portraits of a system
of coupled pendulums
Many of the shapes that describe
non-linear systems are fractal, a set of shapes that are
self-similar on smaller and smaller scales with no limit to the size
of the scale.
Fractals were discovered by
Benoit Mandelbrot at IBM.
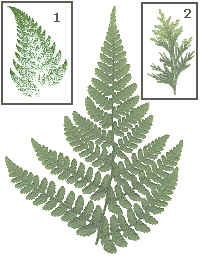
A picture of a real fern and an affine transformation performed by "Winfract"
(Inset1).
Inset 2 is a real
image of a conifer, and bears
an uncanny
resemblance to a diffusion limited aggregate.
Fractals have been seen as describing
naturally occurring phenomena such as the cragginess of mountains or
the shapes of certain plant forms, such as ferns, which can be
modeled by affine transformations.
Whether in fact Nature is fractal, or whether it just describes it
better than the simple geometry of Euclid depends on the
philosophical view taken of mathematics as a whole.
Some people think mathematics is just
a tool or a creation of man, and therefore Nature is only
described or mapped by mathematics.
Others think that the description is real - at least in the sense
that the similarity is not superficial, that in fact natural objects
that look fractal, or which fractals look like, are similar in
appearance because at some fundamental level the natural objects are
obeying some form of rule system that bears a similarity to the sort
of rules which govern fractals.
Whichever way you look at it, one thing no one can say is that
mathematics is irrelevant to Nature.
From butterflies to plants, from the
weather to chemistry, mathematics is modeling or displaying
attributes of Nature, and helping us to understand what we see.
A new conception was being
made... that whatever fundamental units the world is put
together from, they are more delicate, more fugitive, more
startling than we catch in the Butterfly Net of our senses.
Jacob Bronowski
"The Ascent of Man"
How to Float Like a Butterfly
The intricacies of insect flight are
astounding.
But the animals' small size and
swift movements make detailed studies of their aerodynamic
acrobatics difficult. Now results of a study of free-flying
butterflies published today in the journal Nature suggest that
the insects rely on a variety of techniques, often employed in
successive strokes, over the course of a flight.
R.B. Srygley and Adrian
L.R. Thomas of the University of Oxford trained red admiral
butterflies to fly toward a fake flower at the end of a wind
tunnel. Photographs snapped as the insects moved through wisps
of smoke in the chamber provided the researchers with an
opportunity to analyze their flight patterns.
Specifically, the scientists matched
patterns in the airflow around the butterflies' wings to
standard mathematical patterns with known properties. They
determined that the creatures use a number of "unconventional
aerodynamic mechanisms to generate force."
What is more astounding, writes
Rafal Zbikowski of Cranfield University in an accompanying
commentary, is that "the butterflies appear to switch
effortlessly among these mechanisms from stroke to stroke."
Indeed, he concludes, if engineers
ever succeed in understanding just how insects exercise control
over such a wide range of abilities, "there will be a revolution
in aeronautics."
Sarah Graham
[Scientific American December 12,
2002 ]
Butterfly Effects
Variations on a Meme
by Steve Nelson
June 03, 2008
from
ClearNightSky Website
I found a file of search results I had compiled a long time ago as I
was writing scripts to automatically scrape sites based on patterns.
This experiment had to do with the Butterfly Effect, testing some
regular expressions around "a butterfly flaps its wings in..."
The Butterfly Effect
meme itself is invariant, but the
variation in locations and effects is entertaining. My file of
results notes that I did these searches using AltaVista - so that
dates it a bit!
Here are a few of the results:
|
A butterfly flaps
its wings in: |
Causing: |
At this location: |
|
a certain part of
the world |
a storm |
the other side of
the world |
|
Africa |
tsunami |
Japan |
|
Amazonian rainforest |
earthquake |
the other side of
the world |
|
Asian rain forest |
hurricane |
Gulf of Mexico |
|
Australia |
the weather |
Alaska |
|
Beijing |
stock market
flounders |
Wall Street |
|
Beijing |
the weather |
New York City, but
more likely, Queens |
|
Beijing |
win $400,000 |
Montreal Casino |
|
Beijing |
the weather |
Latin America |
|
Beijing |
the weather |
New York City |
|
Brazil |
thunderstorms |
New York |
|
Brazil |
devastating storms
and floods |
England |
|
Brazil |
hurricane |
North America |
|
Brazil |
storm |
Norway |
|
Brazil |
man falls off a
skyscraper |
New York |
|
Brazil |
thunderstorms |
New York |
|
California |
rain |
New York City |
|
Canada |
some impact on the
weather |
south of the border |
|
Canada |
hurricane |
south Atlantic |
|
Central American
rain forest |
the amount of
rainfall |
Chicago |
|
Central Park |
typhoon |
Pacific Ocean |
|
Central Park |
rain |
China |
|
Central Park |
rain |
Peking |
|
Central Park |
rain |
China |
|
China |
hurricane |
Florida |
|
China |
Startup error goes
away |
Descent 3 |
|
China |
the weather |
New York |
|
China |
hurricane |
the Atlantic |
|
China |
enough boomers move
their funds to the bond market to cause the
third derivative of some program's equation for
the market to move from positive to negative |
? |
|
China |
rain |
New York |
|
England |
typhoon |
China |
|
far-away continent |
a development of a
major unstable weather pattern |
half way around the
world |
|
Hong Kong |
hurricane |
London |
|
Hong Kong |
snow |
Miami |
|
Hong Kong |
Internet stocks go
back up |
? |
|
Hong Kong |
effects |
Chicago |
|
Hong Kong |
hurricane |
Gulf of Mexico |
|
Japan |
the weather |
Philadelphia |
|
Madagascar |
the weather |
Cape Town |
|
Malaysia |
hurricane |
Trinidad |
|
Mexico |
hurricane |
Florida |
|
New Mexico |
rain storm |
the Amazon |
|
New York |
hurricane |
Japan |
|
one side of the
world |
hurricane |
the other |
|
one side of the
world |
earthquake |
the other hemisphere |
|
the forest |
typhoon |
Indonesia |
|
this side of the
world |
hurricane |
the other side of
the world |
|
? |
trembles |
universe |
|
? |
moves |
the planet |
|
? |
weather |
China |
|
? |
rain |
somewhere |
|
? |
the weather |
hundreds of miles
away |
|
? |
an ill wind blows
you a $100 bill |
? |
|
? |
something else |
the other side of
the world |
|
? |
stampede of Zebras |
? |
|
? |
hurricane |
the other side of
the earth |
|
? |
the climate changes |
the other side of
the world |
|
|





