by D. Wilcock

from NazirenePeopleOfHonorOnly Website
 

SACRED GEOMETRY

Now that we have given an overview of the entire aether model in this series, and covered some of the basics in terms of how life behaves in the earlier densities, we shall explore some of the physical properties of these densities, and their esoteric connections.

It is important to again remember that these densities are formed by a fluidlike, non-physical energy source. The hard proof for the existence of a fluidlike ‘aether’ is extensive, and will be covered in greater detail in volumes II and III.

First of all, from sources including Ra, we know that the Universe is One.

This One is unilaterally referred to as Pure White Light. It is also referred to as the "seed sound" of the Universe, or the AUM. We are then told that things got rather stale as The One, since nothing really ever changed in this Unity. So, The One decided to create new life from itself. In order to do this, The One vibrated itself into the "octave." The Pure White Light became a series of seven colors - red, orange, yellow, green, blue, indigo, violet. The visible color spectrum embodies the memory of this.

The One Seed Sound broke up into a series of pure tones - do, re, mi, fa, sol, la, ti. The immutable structure of the Octave, those notes which are the purest mathematical ratios and also sound the best to our ears, holds the memory of this. (They can be seen and heard with the white keys on the piano.) Another word for vibration is “harmonics,” and we will frequently use that word to describe these systems.

We need to remember that this Pure Light and Pure Sound are simply two different ways of describing the same vibrations of the fluidlike “intelligent energy” of the One. There is no real difference between them, as they are both functions of vibration. Sound is a vibration of air molecules, and light is ultimately a vibration of the fluidlike aether. We will see in Volume II how Dale Pond has demonstrated that if you multiply the pure sound frequencies many times over, you get the visible color frequencies, thus showing the equivalence between the two.

[Most scientists agree that light behaves like a wave, but they also try to assert that there is no medium that the wave is traveling through – that the wave is simply a particle-like entity known as a “photon” traveling through an empty ‘vacuum.’ This is a preposterous notion, as all natural examples of waves have something that they are ‘waving’ through. The basic definition of a wave is “an impulse that travels through a medium,” and in reality light is no different.]

The third key “harmonic” component that we need to have in place after light and sound is geometry, which is the visible result of vibration. The first and most important geometry that we must start with is the sphere, which the ancient traditions see as the highest geometry in the Universe, the pure essence of the One. In our physics model, the Universe is ultimately spherical in shape, as its energy fields expanded at a uniform rate in all directions as it was formed.

[All of our visible galaxies in the Universe have coalesced into one single “flat” super-galaxy, however, but the spherical energy fields are still present around this super-galaxy, just not as visible.]

A sphere can be compressed into a single point, which has no space and no time, and thus exist as the simplest object in the Universe, but the sphere also is the most complex form in the Universe, containing all other things within itself. Although this might not seem to make sense at first, it is actually quite simple to explain when we start out with a “flat” two-dimensional demonstration, as the ancient students of sacred geometry would learn.

We start by drawing a circle with a compass. Any spot on a circle could be defined as a point, and you could then take a straightedge and draw a line to any other possible spot on the circle. There are literally an infinite number of different lines, angles and shapes that could be drawn within the circle. Mathematically speaking, no other geometric shape can form as many different geometries inside of itself as a circle can, and thus it is the most complex two-dimensional shape there is.

At the same time, its pure, harmonic structure makes it the simplest possible two-dimensional shape in the Universe. It is the only shape where there is only one edge, no straight lines, and a curve that is completely unified for a full 360 degrees around a single center point. It resolves to One, and thus it is the simplest possible two-dimensional shape.

When we expand this into three dimensions, we can then see that the similar principle applies to the sphere.

Confusingly, physicist Buckminster Fuller described a sphere as,

"a multiplicity of discrete events, approximately equidistant in all directions from a nuclear center."

Events, you say?

To put this in drastically simpler language, in a sphere you can draw an infinite number of lines that connect to an infinite number of points (i.e. “events”) on the surface of the sphere, with all the lines starting from one single center point or nucleus, and all the lines will come out to be the exact same length.

This makes the sphere the most complex three-dimensional object that there is; an infinite number of different geometric shapes can be drawn inside of it, by simply connecting different points on the surface of the sphere together. Once you stretch or flatten the sphere in any way, you have less symmetry and thus have less flexibility in what can be geometrically created inside.

(This may seem hard to understand, but it can be proven mathematically. This also explains why liquid naturally forms into spheres when it is in free-fall and/or in a soap bubble, as the air pressure on the liquid is equal on all sides.)

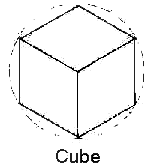
The sphere is also the simplest three-dimensional formation in the Universe for the same reasons as the circle; namely, there is only one edge, perfectly symmetrical in its curvature around a center point, and thus all resolves to One. For comparison, a cube would have six sides or edges, and this is one of the simplest three-dimensional shapes that there is. The sphere has only one ‘side’.

Interestingly, the work of Dr. Hans Jenny has shown that when a spherical area of fluid is vibrated at pure “Diatonic” sound frequencies, i.e. the basic vibrations of the Octave, then geometric forms emerge inside the fluid. Tiny particles that Jenny put in the fluid known as ‘colloids’ would assemble into basic geometric forms during the experiment, leaving clear water in between – where normally the particles would be suspended all throughout the water equally.

If Dr. Jenny turned up the sound frequency to a higher level, then more complex geometric structures would appear, and when he turned it back down to the original level, the exact same geometry that he started with would be seen once again in the same way. This is quite a dramatic demonstration when seen on Dr. Jenny’s “Cymatics” video, which is accessible from various sources – yet such research has been remarkably undervalued and / or ignored by the scientific community.

Thus, geometry is a very basic characteristic of vibration – or as Pythagoras once said, “Geometry is frozen music.”

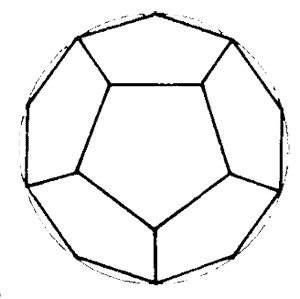
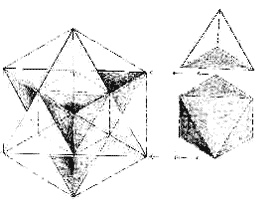
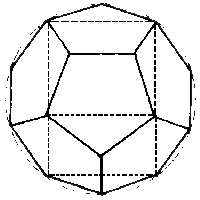
The five most important three-dimensional geometries are collectively known as the Platonic solids, since the Greek philosopher Plato first wrote them about in modern times.

As one note, the label “St. Tetrahedron” is an abbreviation for “Star Tetrahedron,” or what is more technically known as an interlaced tetrahedron.

You can also examine the tetrahedron by itself, which is simply a four-sided pyramid with equilateral triangles on each face, but in terms of the workings of energy as vibration, it appears that most tetrahedral structures have two tetrahedrons stuck inside of each other as we see above.

There is clear evidence that any scientific effort which moves towards a discovery of the importance of these geometries in the Universe is being actively suppressed, as those in the secret brotherhoods still have a high degree of power and feel bound to “ever conceal and never reveal” the “secrets of the Order.”

Many of these group members have deliberately arisen to power in various scientific institutions, and are thus positioned to deflect certain types of research, especially those related to free energy / anti-gravity, as we shall discuss in Volume II.

Richard Hoagland and the Enterprise Mission, working with Lt. Col. Tom Bearden, have shown how such suppression efforts trace back to the 19th century, at least. The great 19th century pioneer who analyzed the behavior of the electromagnetic (EM) wave was Sir James Clerk Maxwell. His equations, known as “quaternions,” were used to map out the full, hidden internal structures of the EM wave in full 3-D view, with over 200 equations altogether.

When you analyze all 200+ quaternions as a group, you see the geometry of a tetrahedron inside a sphere. This is the hidden secret of the electromagnetic wave, the underlying structure that determines its behavior as it moves along – and Oliver Heaviside and others, who reduced Maxwell’s equations to four basic quaternions and declared the hidden geometry to be “occult nonsense”, vigorously removed it from all academic debate. Had this not been done, we may have “solved the puzzle” far earlier along.

There is no direct way to prove that those from the secret groups inspired this political move on Maxwell’s work, but it is exactly what we would expect based on their own system of beliefs that they are sworn to uphold on pain of death. An even more obvious example was the demonizing of the “aether” concept through using the results of the Michelson-Morley experiment as “proof.”

19th century mystic Madame Blavatsky predicted that the aether would be removed from discussion, and that,

“the pillars of science would come down along with it.”

Even now, the anti-aether bias is so strong that you will be almost immediately dismissed if you try to bring it up in a scientific discussion – but we are not concerned, as time and proof will heal this wound.

Once we do accept the existence of a fluidlike aether at various levels of density, where each density has a different quality of vibration, then we realize that certain clear geometric forms will emerge at the various “pure” frequencies. Indeed, geometry is the single most important aspect of the aether’s behavior in terms of being able to construct stable structures, such as crystals.

Without the geometry, matter would not be possible, as geometry is what allows the “field bubbles” of the aether to clump together in precise, organized patterns, forming specific molecules. Otherwise, the best we could hope for is that the spheres would line up pole-to-pole, and otherwise be free flowing around each other – and this behavior would not be complex enough to build matter.

The tips of the geometries have more strength to attract each other than the other areas on the surface of the sphere, as we shall discuss below, and this allows the spheres to organize into non-random “matrix” patterns.

Though we cannot directly see these geometries most of the time, except in crystal structures, microclusters and quasi-crystals (volume III), they create distinct “stresses” or pressure zones in the aether that can exert enormous forces on their environment. Think about the force that is contained in a whirlpool and you’ll see how a fluid can have areas of stronger and weaker force inside of it.

These geometric forms therefore possess both qualities of a fluid, as they are forming in a fluid medium, as well as a crystal, as they are clearly geometric – hence Dr. Harold Aspden refers to them as “fluid crystals.”

By the end of Volume III, we will have constructed a complete physics model to demonstrate how these formations are hidden within all physics, whether quantum, biological or cosmological. If you think the science of chemistry and quantum physics is complete as it is, you will be very surprised to find out how many problems there are with the current models – and that the design we present here solves every one of these problems.

In this book we will cover some of the basics of how this geometric patterning works, including the “Global Grid” of energy lines on the Earth, which directly shape the continents.

The most important quality of the Platonic Solids is that each shape fits perfectly into a sphere, such that all its outer points precisely merge with the outside surface of the sphere. Each of the straight lines that make up these objects will be the same length, and all geometric points on the sphere’s surface are equidistant from their neighbors – which is exactly what we would expect with the science of vibration.

Plato and other Greek philosophers also pointed out that all the angle measurements in these geometric solids are the same, and that each side of the three-dimensional objects have to be the same shape. Although this may seem confusing at first, it actually works out very nicely. There are only five major shapes to contend with when we look at this information. Those five shapes are the octahedron, star tetrahedron, cube (hexahedron), dodecahedron and icosahedron.

In order to understand why such geometric objects form inside a vibrating sphere of fluidlike energy, we have to know a little about wave movement. If we have a simple two-dimensional wave, such as a vibrating guitar string, then there are three basic components that will stay the same if the wave is not disturbed. These three basic components are the wavelength, the frequency and the amplitude.

The wavelength is how long each part of the wave is, i.e. “the observed distance between two adjacent wave crests,” (measured as a length quantity in angstroms when dealing with visible light.) The frequency is the number of wave crests that pass by an observer each second – measured as cycles per second or “hertz,” and the amplitude is how high each wave is – i.e. “the size of the wave measured from zero to peak.”

Any color or sound that stays the same for a length of time will have a continuous repetition of the same wavelength during that time. As a typical example, the “concert-level” frequency for the note A is 440 cycles per second. This means that when air vibrates 440 times in one second, our ear interprets this as the musical sound “A”.

That’s all there is to it. If those 440 cycles didn’t all have the same frequency and amplitude, then we wouldn’t hear a steady pitch at a steady volume. If we increase the frequency of the sound, such as by going up to 497 cycles per second, then the pitch will go up as the wavelength shortens. If we increase the amplitude, the volume of the sound will go up as the height of the wave increases, but its pitch will stay the same.

We should also remember that complex information can be stored in these waves. We have two types of waves that are used for radio: frequency modulation, or FM, and amplitude modulation, or AM. The word ‘modulation’ simply means ‘changing.’ So, as a simple explanation, the FM waves stay at the same amplitude but have continuing changes (modulations) in their frequency, whereas the AM waves maintain the same frequency but have continuing changes in amplitude.

That’s basically all there is to it. Since these electromagnetic waves can move so fast, there is a great deal of information that can be stored within them – and that is an important point. The encoded information of AM/FM radio, CB, the police/fire/emergency bands, broadcast and satellite television stations, cordless and cellular telephone conversations are always around us in every moment.

Now when we have a three-dimensional geometric waveform inside of a sphere, the wavelength and frequency would be represented by the distance between the various node points across the surface of the sphere, which could be measured in degrees, and calculated by the sine function in trigonometry. The amplitude would be measured by the size of the sphere, which could be measured in radians, and calculated by the cosine function.

Thus, as we pump up the strength (amplitude) of a given spherical energy field, so too will we increase its size – which explains why these structures exist from the tiniest level of quantum mechanics all the way up to the known Universe. It is also important to realize that in this fluidlike aether system, increases in frequency will also draw in more aetheric energy from the surrounding environment, and thereby increase the size (amplitude) of the sphere as one geometry shifts to another.

We will explore this later in the chapter, when we see how neatly the different Platonic Solids “nest” inside of each other, with each new geometry larger than the one inside of it. So typically, a frequency increase will also involve an amplitude increase.

The only thing left to explain is why the vibrations form tips or points or vertices at the surface of the sphere, with straight lines connecting them. Again, returning to a the simple study of a wave in two dimensions, known as wave mechanics, we know that every wave has certain points known as “nodes” where there is no movement. This is easiest to see with the basic sine wave, which is shaped like a slow-moving wave on the surface of a lake – a continuing S-shaped curve. If you pluck a guitar string, there are certain areas of the wave where there is no movement at all, but it actually will remain perfectly still.

These areas are the “nodes,” and you obtain the wavelength by measuring the distance between these nodes. A node could also be seen as the area where a child’s seesaw is supported by a metal pole; either side of the seesaw can go up and down, but the middle of the board will always stay in the same place. Again, such a point is known in wave mechanics as a “node” or a “moment point.”

Similarly, the pointy tips or vertices of the Platonic Solids represent the nodes of the wave.

These points are where the least amount of vibration is occurring throughout the entire sphere. Consequently, we will see that in this “stillness” is great power, caused by the pressure surrounding the points. These node areas (as well as the exact center of the sphere) actually have the greatest energetic strength across the entire surface of the sphere, because the surrounding higher-pressure zones of vibration will naturally gather up and direct everything “loose” in the area back to these low-pressure zones. It is for this very reason that the most number of loose “colloids” would gather into these nodes in Dr. Jenny’s experiments.

(This is also the same reason why high-pressure storm clouds will rush into a low-pressure zone in our atmosphere.)

Since these nodes exert great force on each other by the laws of vibration, then as the old saying goes, “the shortest distance between two points is a straight line.” So, straight lines of force are naturally formed between these nodes once they are created, and when you see all the lines combined together, the geometric object emerges – just like connect-the-dots.

The last terms from wave mechanics that we need to introduce at this time are “moving wave” and “standing wave.” (The terms “dynamic” or “propagating” for the moving wave and “static” for the standing wave are also used.) This is quite self-explanatory – a moving wave moves through space, where a standing wave stands still as it vibrates. So, if we have a sphere of fluid that remains stationary and has a geometric stress pattern of vibration inside of it, that geometry is referred to as a “standing wave.”

Once we think in these terms, it becomes easy to put the model together – it is based on simple, known physical principles of vibrating fluid, and the quasi-solid “stresses” that can be formed inside of it by vibration.
 

MATCHING UP GEOMETRIC FORMS TO THE “DENSITIES”

Now if we think back to the idea that there is an Octave of aetheric densities in the Universe, we can see that these densities have color, sound and geometric components.

This is perhaps the most frequently studied connection that was explored by the inheritors of the ancient mysteries, long after they had lost track of the full scope of scientific knowledge that was behind it.

So, one early puzzle that we worked on from 1996 to 1998 was,

“How do we assign a geometric shape to each of the seven major densities, since there are only five Platonic Solids and the sphere to work with?”

We do not need eight shapes, as the ancient traditions tell us that the sphere exists both at the beginning and the end of the Octave.

Similarly, in the Octave of sound, any note that is an octave higher than another note will sound the same, just in a different register – a higher or lower octave. Mathematically, any musical note that is an octave higher than another note will have exactly twice as many cycles per second – so “A” at 440 cycles per second will again become “A” when it gets to 880 cycles per second.

So where is the seventh shape?

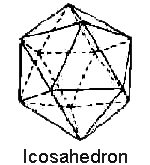
The answer was found in the “religious myths” of the ancient Vedic scriptures from India, the remnants of the Rama empire, as told in Robert Lawlor’s invaluable book Sacred Geometry. The Hindus, or their contacts, supplied the answer by supplying us with one of the Platonic Solids twice. Just as the sphere appears twice, at the beginning and end of the octave, so does its closest harmonic partner, the icosahedron, located at the second and seventh density levels.

For the rich, mystical culture of the ancient Vedic texts, with the full cooperation of extradimensional entities flying about in fabulous vimanas, the icosahedron shape was actually turned into a god.

They named him Purusha, and in the seventh dimension, or density, he represents the masculine force in the universe.

As we just said, Purusha also shows up as the first shape for the sphere to crystallize into when we are at the beginning of the spectrum.

Therefore, the One, being a manifestation of all conscious entities, must crystallize down into the world of form as Purusha, and any entity must again attain the level of Purusha to return to the One at the end of the cycle.

The next image from Lawlor’s Sacred Geometry shows how you would draw an icosahedron in two dimensions, using a compass and straightedge.

Before we assert that the Hindu culture was sexist and male-driven, assigning masculinity to all the best spiritual forces in life, realize that there is a yin to our yang.

The universal feminine force is referred to as Prakriti, and is identified as the dodecahedron, or the sixth density.

In fact, it appears that each density can be considered as having either “male” or “female” qualities, the second being female, third male, fourth female, fifth male, et cetera. Let us not forget that the Oneness is a combination of both genders in Unity.

Thus, as Purusha starts as female in the second density, we see that it is, indeed, a father / mother god, also encompassing the feminine, or Prakriti archetype within itself. Once we read further into the design and understand the metaphysical and spiritual properties of the dimensions, their “genders” will make tremendously good sense.

Other than the sphere, we can see that Purusha and Prakriti are the two highest shapes in the spectrum, so it makes sense, in some way, that these two shapes themselves could have been personified as gods and goddesses. These higher realms are clearly something we can aspire to, and these are, essentially, conscious shapes.

Our own home is currently in shape number 3. This, the octahedron, is the vibratory level that provides the invisible background framework for the energy that all of our atoms and molecules are created from. Rod Johnson, whose sacred geometry model of quantum physics, has asserted that the massless "neutrinos" that have been observed in the laboratory could well be octahedrons.

However, more often than not these vibrations would remain undetectable, as they are only the underlying framework of reality, not the actual reality itself. When you look at a finished skyscraper, you don’t see the I-beams. Similarly, we don’t see the "zero-point energy" that creates "virtual particles" of protons, neutrons and electrons which constantly wink in and out of existence, but yet we know that it must exist.

Therefore, the ancient physics would teach us that this shape represents the fundamental background for all matter in our "density."

This is the forgotten ancient teaching. It is important to realize that this is only a general rule, as within our own density we see evidence of all the Platonic Solids, representing the different “sub-densities.”

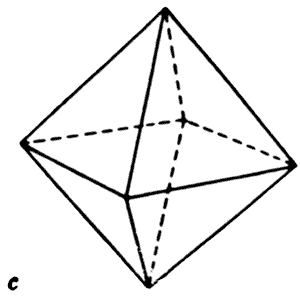
We need all of them in place to be able to build physical matter – but the strongest one in third-density is the octahedron.

To look at just the top half of an octahedron, we can easily see that it is identical to the shape of the Egyptian Great Pyramid.

With the full physics model in place, this simple fact will clearly illustrate that all pyramids were designed in order to be able to focus this geometric energy of the aether, much as would a funnel direct a flow of water.

As we will see later in this volume, the “torsion fields” on the Earth can vary from place to place far more than the normal “push” of gravity or of the Earth’s magnetic field, and in the Russian lingo, any pyramid acts as a “passive torsion generator.”

Matter itself behaves like a vibrating sponge that is submerged in water, with fluidlike energy continually flowing in and out of it with a pulsating motion. When you clump matter together into a single structure, the shape of that structure will determine how the aether “currents” flow through it. Any cylinder or cone-shaped object will harness and focalize torsion fields, as we have extensively documented in Volume III.

There are always torsion fields coming out of the Earth in spirals, and the cone shape can direct and focus these fields. Let us not forget that these fields are composed of intelligent energy, so one major benefit of harnessing these fields is that they will dramatically enhance your physical health as well as your spiritual consciousness in a short time – hence the ancient Egyptians referred to the pyramids as “temples of initiation.”

And we know that the Greek word “Pyramid” is a conjunction of the words “Pyre” and “Amid,” meaning “Fire in the Middle.” This “fire in the middle” represents the energy fields that are harnessed inside the Pyramid – hence the name itself conceals part of the secret.

In essence, with the proper science in place, we realize that the Great Pyramid of Gizeh, the most precisely constructed pyramid on Earth, is a fantastic machine, fashioned with a technology that is far more advanced than our present scientific level of understanding. The reason why is that this is a technology of consciousness, working off of a physics model that we are only just now rediscovering in the public arena. And the more that we examine the Pyramid, the more that we can see how accurate and comprehensive the ancient knowledge that went into it must be.

It is an established, longstanding fact that if you take the difference between the base and height measurements of the Pyramid, the pi ratio of 3.14159 is expressed. This means that you could draw a circle from one corner, over the top and down to the opposite corner, and that circle would perfectly touch all three points.

Then, all we have to do is think in three dimensions, and we will quickly discover that the Pyramid mathematically fits perfectly within a half-sphere.

So, in a very direct fashion, the pyramid structure forms “resonance” with the aether, causing a sphere of unseen energy to form around itself just like this.

Remember that the strongest geometric energy structure of our own dimension, if we could see it, would look exactly like this. Thus, the Pyramid was not only a geometric object, it was literally built as a giant, solidified “consciousness unit.” On one level, we could think of it as a giant statue in honor of the energy density that we now inhabit – but it is also a very potent machine. We have also been told by Ra that it was far more effective when it was first built than it is now, due to the changing positions of the Earth and the deterioration of its stone faces.

Many Pyramidologists have pointed out that the outside of the Great Pyramid expresses the exact length of an Earth year, 365.2422, in many different measurements.

Since scholars understand that the Pyramid perfectly fits into a half-sphere, many have concluded that the Pyramid is designed to represent the Earth. But that wouldn’t explain why the pyramid builders didn’t simply erect a globe, especially with the apparent technology that they had at their disposal to precisely position such huge stones. It is only now that we can see why the octahedral form was chosen in order to do this.

Though we cannot see the Pyramid as a crystal now, it is a well-known fact in Egyptological circles that when the Pyramid was first built, it was entirely covered on the outside with casing stones.

These were made of white Tura limestone that was precisely mirror-polished to a glowing sheen (Lemesurier, 1977.) It was so bright in daylight as to be blinding, hence the ancient Egyptians named it “Ta Khut,” or “The Light.” It would be very easy to conclude that it was not built by primitive human beings when seen in this original form.

In the next picture below, we see the remnants of these stones that still exist along the bottom.

What is not often known is that the spaces in between these casing stones were only 1/100th of an inch wide (Lemesurier, Hoagland.)

For comparison, the best that modern technology could do to align the heat shield tiles on the Space Shuttle was one thirtieth of an inch tolerance (Hoagland.) This puts the fashioning of the casing stones on the level of optical precision; something we would normally only use for extremely sensitive pieces of equipment. All of this precision was used to make it that much more effective as a “machine” that harnessed torsion fields.

Furthermore, in these incredibly tight spaces between casing stones, so tight that a knife blade cannot be pushed into them, there is an impossibly thin layer of “cement” holding them together. This “cement” is so strong that to strike the joint with a sledgehammer, the limestone itself breaks before the “cement” does.

Still to this day, no one has provided a satisfactory explanation for how this could have been done. It certainly appears that the stones themselves were fused in place, and thus it wasn’t cement at all, but a product of extreme heat, melting the two stones together. So how did they get the heat? A laser, perhaps? Or was it focused consciousness, transforming the matter phase of conscious limestone molecules?

Ra’s explanations start to make more and more sense to us as we go along, as in their model, they were able to use consciousness to visualize how they wanted the stones to arrange themselves, and their visualizations would then become reality.

To summarize, then, the outside of the Pyramid was fashioned with an optical precision that is only now matched by the type of work that we would do on a mirror lens for a reflecting telescope (Hoagland.) We must then picture a giant pyramid built out of four mirrors, so bright in the daylight as to be almost blinding.

Again, it is no wonder that ancient Egyptians referred to it as “Ta Khut,” or The Light.

When it was in its true crystal state, there could be no doubt that it was not built by the humans of the time; it would be a most totally alien-looking structure. We can only imagine its original appearance now, as earthquakes jarred most of the casing stones loose in the early years of the first millennium AD, and these perfect white stones were then hauled off to build mosques in Cairo. Thus we can only measure the original design of the casing stones from the few that remain along the bottom, still intact.

The top of the second pyramid also has some casing stones still remaining.

This almost insane degree of precision starts to make a lot more sense when we realize what energies might be able to be harnessed by the building of such a structure. These energies would not be cold and lifeless like electricity; instead, they would represent conscious energy, and could thus be directed by a conscious human being, once trained.

The author’s own sources, along with Ra and the Cayce readings, indicate that a person well trained in directing this energy could rejuvenate dying bodies to extreme youth and vitality, travel in time and levitate massive objects with ease.

Furthermore, it helped to stabilize the Earth on its axis, decrease severe weather and earthquakes in the surrounding area, heal and normalize the mind, purify water, create usable energy and eliminate leftover radiation from nuclear battles in much shorter amounts of time. The more we learn about the science that is involved, the more obvious this will become – and the greater of a desire we will have to rebuild a worldwide network of pyramids once again to heal the earth of the present damages that we are creating.

Indeed, Ra tells us that the Pyramid was a giant gift that they produced for our civilization, a gift whose primary purpose centered on providing a temple for initiation while also functioning as an effective balancing agent for the Earth’s energy fields.

Having a “temple of initiation” meant that higher-level energies could be harnessed and integrated into the physical and nonphysical bodies of the human seeker, and the full soul evolution progress through the spectrum of seven densities could then be made while still on Earth. This was a very rigorous and terrifying process, as one essentially confronts all of the “distortions” of the personality self at once, in what amounts to a subjectively long-lasting nightmare.

A trained healer, who can travel with the person out-of-body while they go on this journey, was always present for this work to be done, since the fear alone could cause the person to lose track of the physical body and thereby die.

If the initiation was successful, then after such a progressive evolution is complete, that entity would have access to all the power of the entire octave of dimensions, becoming like a god and having Christlike abilities, if it decided not to leave the Earth. One reason that the inheritors of the Atlantean Mysteries felt that they had to keep the knowledge a secret is that they felt that if a negatively-polarized person made sufficient progress in the Pyramid, they could become a very powerful force of evil on Earth – even though it appears that this would not truly be possible, since the negative path cannot sustain itself above the fifth density.

It should be no surprise that mystical tradition long holds that Jesus also completed a Pyramidal initiation in such a manner, and might well have been the only person coming in well equipped enough to actually complete the process in full.

According to the Edgar Cayce readings, Jesus enjoyed a former lifetime as Hermes, the co-designer of the Pyramid with the priest Ra-Ta, who later reincarnated as Cayce himself. Thus, it appears that Jesus later utilized the very piece of technology that he originally helped to build, in order to complete his own initiation.

As we will see in the end of the book, the Pyramid actually wrote Jesus’ arrival directly into a timeline based on a geometric and numeric code built into the design of the chambers and passages inside. The prophetic statement of this Messianic arrival occurs at the moment where the narrow Ascending Passage suddenly heightens tremendously into the Grand Gallery. This particular event in the Pyramid symbolism is arguably one of the single most powerful symbolic events of the entire span of time given. Obviously Jesus knew, even as he helped design this incredible structure, what he would later use it for in future lifetimes.

If the pyramid shape is a basic product of understanding a more advanced physics than we are now using, then we would expect that the technology would be discovered by any civilized society on any inhabited planet.

In 1981, Ra said that Mars is the only remaining planet in our Solar System that had third-dimensional humanoid life like ourselves in any recent past. And in the late 1980’s, Richard Hoagland’s work began to be more widely known, which did indeed reveal the remnants of just such a civilization.

From Hoagland and others’ data regarding Mars, we see that the largest and easiest pyramid to identify in the Viking-photographed Cydonia region of Mars is five-sided, almost precisely duplicating the top of an icosahedron, or the Hindu god Purusha, if we remember. Near this five-sided pyramid is a city complex of slightly smaller pyramids that appear identical to those we see in Egypt.

In addition, the Mariner-photographed Elysium pyramids on Mars are clearly in the form of tetrahedrons, and Carl Munck, demonstrates a North American Earth mound in the form of a tetrahedron in his book The Code, also available from the Laura Lee Online Bookstore. Furthermore, Hoagland and others have written of spherical glass domes on the Moon, which might well serve the same purpose in harnessing torsion fields, holding in an atmosphere and providing a clear view of “outer space.”

Our own ex-NASA astrophysicist Maurice Chatelain, whom we also shall discuss in later chapters, came forward in 1995 with the shattering revelation that NASA had found "geometric ruins of unknown origin" on the Moon during the Mariner and Apollo missions.

More recently, similar testimony was given at the Disclosure Project conferences, starting on May 9, 2001 – and we attended the May 10 event and personally interviewed the witness.
 

GEOMETRIC ENERGY TRANSITIONS

Our next question is, “How do we naturally map out the transitions from one geometric energy frequency to the next?”

Through a moderately complex set of procedures, one can demonstrate how each geometric form will naturally “grow” out of the one before it. To begin with, the sphere into the icosahedron is relatively obvious – the movement of formless Unity into geometric form – so there is no real modeling to be done. The second-density icosahedron into the third-density octahedron will be clearly modeled in Volume II.

In order to turn our own octahedron into the shape of the 4th dimension, all that is required is to expand each face into a basic four-sided triangle, or tetrahedron. In our diagram here, we conceptualize it as if you were going to place a tetrahedron onto each face separately.

Each face on the octahedron, which is in the form of an equilateral triangle, (composed entirely of 60-degree internal angles, with each side the same length,) becomes one three-sided tip of a star tetrahedron.

As the octahedron has eight sides, you would then need to add eight tetrahedra to its faces. To animate this progression like a cartoon, it would appear that the octahedron was suddenly blooming like a flower; the faces suddenly sprout upwards as the tetrahedra rise into position.

[Compare the diagram here with the original harmonic table in order to help visualize this. The top right shape in the diagram shows where one of the eight tetrahedra would be, in terms of position, if it were not attached directly to the octahedron.]

In order to then progress from the fourth dimension to the fifth, you can look at the diagram and easily see how a simple connect-the-dots on the edge points of the star tetrahedron forms the cube.

To go from the fifth-dimensional cube to the sixth-dimensional dodecahedron, a further outward expansion is required, where each face of the cube sprouts an inward-slanting "rooftop" in order to turn into the dodecahedron.

The "roof" shape that appears is most easily seen in the rectangular area below, whereas the square area would be more akin to an overhead view.

Then, if you put a dot in the center of each pentagon on the dodecahedron and connect all of the dots together, you will have a series of lines that form five-pointed stars that create the icosahedron shape, the last major node before the return to the Sphere.

In short, going back to our original harmonic table again, we can see how the entire progression is a sphere, or a Oneness, expanding into the “seed” or fundamental form of the icosahedron, which then by its structure gives rise to all of the other forms contained therein (Lawlor, 1982.)

The "seed" aspect of the icosahedron is why the Hindus associated it with a male god - they were using the metaphor of the semen, or "seed of life."

What we have here is an understanding of the fact that the shapes formed by these energy vibrations can grow, much in the way that crystals grow.
 

ALL IS ONE

We shall briefly cover another point that has been a major source of confusion to those reading this book, and attempt to break it down into simpler terms in this revised edition.

If you still find it difficult to understand, just be reminded that it isn’t an essential point that is needed to understand the physics. In order for the Universe to truly be One, there must be a level where there is no space and no time – where All is Here and Now. Sources such as “Seth” through Jane Roberts tell us that nothing in the Universe really ‘exists,’ including the aether itself – that all the Universe is expanding and contracting from a single point of Oneness in each and every moment.

So, the many tiny “field bubbles” that make up the fluidlike aether appear to flow around each other when we study their behavior. On one level, this is indeed true, as the experiments of Dr. Nikolai Kozyrev, Nikola Tesla and others have demonstrated, which we will cover in Volume III. On another level, we must remember that the amplitude of the spherical wave shows us that the “zero point” of the wave is indeed right in the center, meaning that the wave itself is constantly expanding and collapsing from a single point.

Think of a balloon that is constantly inflating and deflating from a very tiny point to a very large sphere.

At the highest level of vibration, all of the energy in the sphere is contained within the central point. Though this does seem confusing, various sources such as Seth and Ra tell us that all of those single points are actually joined together in Oneness – that there is only one single point that all is emanating from. This is another way that we can understand that we do have a perfect “spark” of the One Infinite Creator within ourselves.

If this is true, and we have every reason to believe that it is, then each of the geometric shapes that we have discussed must be continually present, at their own frequency, in every “consciousness unit” or field bubble in the entire Universe. Roughly speaking, every energy form is pulsating from a point, through the icosahedron, into the octahedron, to the star tetrahedron, to the cube, to the dodecahedron, again to the icosahedron, and again back into the sphere or point once more.

This is the only way we can explain that Seth would tell us, loosely paraphrased, that,

“your entire reality system is “off” as much as it is “on,” and you simply do not vibrate quickly enough to see what is in between the gaps.”

Another analogy that we have used is the idea of a filmstrip.

The actual filmstrip in a movie camera is a series of still pictures that are separated from each other, but when we watch them fast enough, they form “moving pictures,” or “movies.”

So, the spherical energy that forms the Universe itself could be seen to vibrate through all the different shapes at mind-numbing speeds, forever expanding from a single point out to form the boundaries of space and time as we know it and then compressing back into that space yet again just as quickly. Although it seems almost impossible to conceive of our entire universe as crumpling up into a single point over and over again at speeds too fast to measure, this is exactly what is happening, say sources such as Ra.

Since all of physical reality is ultimately nothing but conscious energy in vibration, each density would then have the illusion of only existing at one level in this energetic system. In fact, all of the densities are interpenetrable, and the vibrations from higher densities will exert measurable stresses in space and time here in the third.

Among other things, this forms the basis for the Global Grid, which we will examine in future...