The Fractal Matrix
A Paradigm For Multidimensional Reality
PART I
(June, 2004)
Clearly there will be great difficulties with this subject and
consequently there will only be degrees of understanding. Such a model
has to have a framework which underlies all existing knowledge and experience,
ranging from the God concept to the trivial. It should explain, handle or embrace
all fundamental issues, for example:
-
systems from the micro to the macro
-
holistic
properties
-
unity/polarity
-
quantum reduction (a feature of quantum mechanics)
-
chaos theory
-
fractals
-
nature's computer programmes
-
consciousness and free
will
-
subjective/objective relationship and hierarchical, holographic and gestalt
properties
-
synchronicities
-
higher dimensions
-
God concept and theory of One
-
emergent software
-
context
-
qualitative/quantitative
-
the relationship between
the part and the whole
-
time, etc...
The reader may wish to study first the author's
article
Time as an Infinite Fractal, since time manifesting as an
infinite fractal arises from the infinite fractal aspect of energy. Note that
although the phenomenon of fractals, first evaluated in the 1960s by Benoit
Mandelbrot, was considered by some to be the greatest discovery in mathematics,
it is even more significant, with far reaching applications.
The heart of the difficulty is that our minds are formatted
for linear operations in this third dimension. Moreover when we extend this
into nonlinear (inner) perceptions such as in art and music appreciation but
also in many underlying concepts to intellectual pursuits, and then attempt
to observe this more holistic state of mind, it breaks down (quantum reduces)
to the ego-conscious observer reality of the physical sense perceptions (the
parts within or representing the whole).
In other words, we can't observe analytically,
a state of unity and multiconnected phenomena, since the objective observation
process breaks them down into linear parts. It is important to stress how difficult
this material is otherwise the point will be missed by many.
If we think of ourselves on a single 2D flat plane, movement
and thought along this plane would be what we are calling linear. Nonlinearity
would come in from imaginary countless other layers superimposed 'above' our
familiar single linear plane. In reality though, it is not 'above' but in expanding
spheres (concentric circles in 2D).
In truth each point in our plane is influenced by the upper
levels. We are merely introducing the subject by means of simple examples or
analogies. In effect the behaviour of a particle or a living entity on the bottom
plane is governed ultimately by the whole of the countless layers. This is where
the real difficulty arises; to obtain some grasp of the effect of infinitely
superimposed nonlinear variables. This is the key problem in understanding the
mind's (or universal or nature's) computer system.
Perhaps a very simple analogy depicting only two variables (in
fact only one nonlinear variable) would help; that of taking the dog for a walk.
The dog's behaviour represents the external view of our material world of physical
senses or the first plane. The human (upper plane) represents a higher order
of control. The leash links the two together and determines the boundary conditions
imposed on the bottom plane (the dog).
The longer the leash, the greater the
gap between the levels and the more freedom the dog has. This also means the
more probable choices it has relative to the human's control. Moreover, we see
that the decisions of the human are superimposed on those of the dog, and the
dog's behaviour acts within the context of the human's control. If one
could observe only the dog (analogy: external world), its activity could not
be understood without taking into account the superimposed human control (higher
order, for example, soul level).
This gives the reader an idea of the resultant effect of only
two combined variables---the dog's control and the human control. These are
each equivalent to fractal levels. Also the dimensional gap between two such
fractals determines how much randomness there is between the two fractal levels
or how many probabilities there are for selection (choices, freewill).
The longer
the leash the more possibilities the dog can experience on its own, but note
that it then has less guidance and it is in effect more disconnected. We can
refer to the lower level control (the dog's) as local control (LC) and the upper,
as global control (GC). LC is always in the context of GC. But this GC becomes
local relative to a greater GC. All LC and GC programmes occur at fractal levels.
What would be the most simple structure for the initial development
of such a model? It would be a circle. Let us now elaborate on this circle and
make it into a spiral; a little like connecting together many circles---see
Figure 1. This should be imagined as a fine spiral with no gaps (beyond about
quantum size).
 In
2D they are like circles within circles but in 3D or more they are like shells
within shells connected as a total spiral (ideally this should then be envisaged
in 4D to give perfect super-symmetry when we introduce the anti-spiral). This
is the same as the vortex model given in other articles where much more detail
is presented, such as the article,
The Basic Energy Unit ---which, in
particular, shows the higher-dimensional nature of the vortex.
In
2D they are like circles within circles but in 3D or more they are like shells
within shells connected as a total spiral (ideally this should then be envisaged
in 4D to give perfect super-symmetry when we introduce the anti-spiral). This
is the same as the vortex model given in other articles where much more detail
is presented, such as the article,
The Basic Energy Unit ---which, in
particular, shows the higher-dimensional nature of the vortex.
In terms of three or more dimensions, this spiral would resemble
spheres within spheres. The direction of motion of the energy is inwards from
be periphery to the centre. This is essentially a model for a vortex. Current
science interprets reality at the particle level and thus focusses only on the
external world and the lowest contextual orders of the spiral near the centre.
What logical justification do we have for introducing these
concentric circles or spirals? The spiral or vortex is a natural and efficient
way for energy to transduce from higher dimensions to low. The reader is referred
to the articles,
The Source of Fractals and
The Theory of One.
Returning to Figure 1, what may be surprising now is that each
turn of the spiral (a circle) is a potential fractal level. Figure 2 shows three
potential fractal levels highlighted---meaning they have manifested a form into
reality. If we imagine an opposite total spiral underlying the one in Figure
1---see Figure 3, a 'side' view---using the 2D or 3D view of this, we can give
it standing wave structures at each of the levels where the opposite interacts.
(There are no stable forms or even time without counteraction and limitations.)

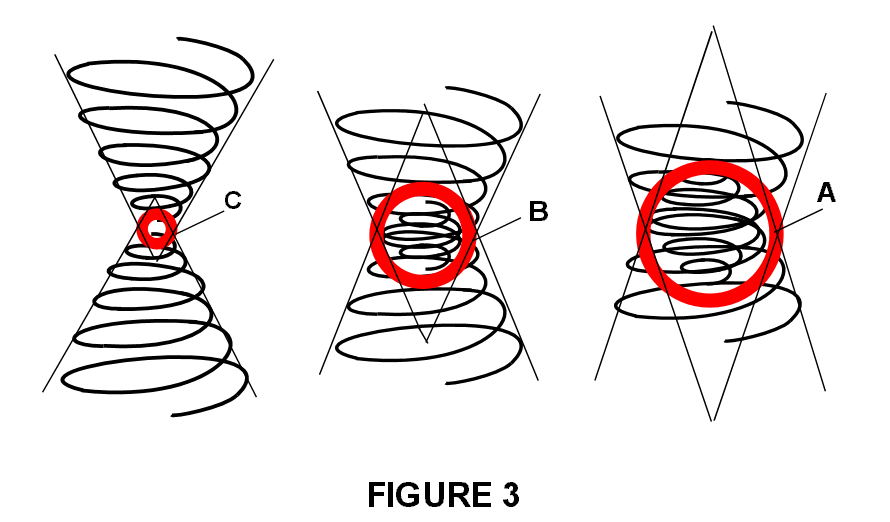
Figure 2 shows the three fractal shells formed by opposing spirals,
creating standing waves. Figure 3 gives an idea of the inner structure. Since
this has been covered in other articles we will not repeat the explanation as
we wish to move on to programming applications to nature and the universe.
In effect, we are describing a vortex matrix from which all
forms emanate. In Figure 2 the fractal strata A, B, C could be a universe, a
planet, an atom, respectively. One might see at this point that the universe,
circle A will spiral through other fractal levels, not shown: into many galaxies,
which in turn spiral into many star systems, which in turn spiral into planets,
such as fractal level B in Figure 2, and further eventually into atoms, say,
fractal C (see later figures).
These must be stable stationary states---and
there will be many in reality. Note that the spiral forms closed systems at
these fractal levels (which on the negative side provide a mechanism of entrapment
and evolutionary control).
 Figure
4 gives another view of this. The top represents the unity of everything below
it, and corresponds to A. Then B and C are levels further down.
Figure
4 gives another view of this. The top represents the unity of everything below
it, and corresponds to A. Then B and C are levels further down.
Figure 3 shows the connection between the spiral and the anti-spiral,
and is a 'side' view of Figure 2. The next feature we need to mention is that
each spiral circle in Figure 2 functions in the context of the next higher (larger
circle) context. For example the fractal level B, say, a planet, will regulate
the order of the lower fractal level of atoms at C. Also the dimensions and
frequencies increase towards the greater spiral circles.
The significance and
meaning of dimensions and frequencies is not easy, except to recognize that
the probabilities increase with the widening spiral, that is, greater degrees
of freedom, greater number of choices, increased variety, etc. The centre circle
of the spiral (Figure 3) would represent a particle or a world made up of these
units; this centre circle is the manifestation region of the interacting spirals
and can be any level such as A, B, or C, where stable standing waves are formed.
So far then we have one big spiral or vortex (with its opposite),
which splits up into a myriad of smaller ones---we need many smaller circles
to make up a reality. When a split occurs, this forms new fractal levels of
stability or existence---the atoms, the planet, universe, in Figure 2. Figure
5 illustrates the multiplication of these spiral fractals---anti-spirals not
shown---and can be compared with Figure 4.
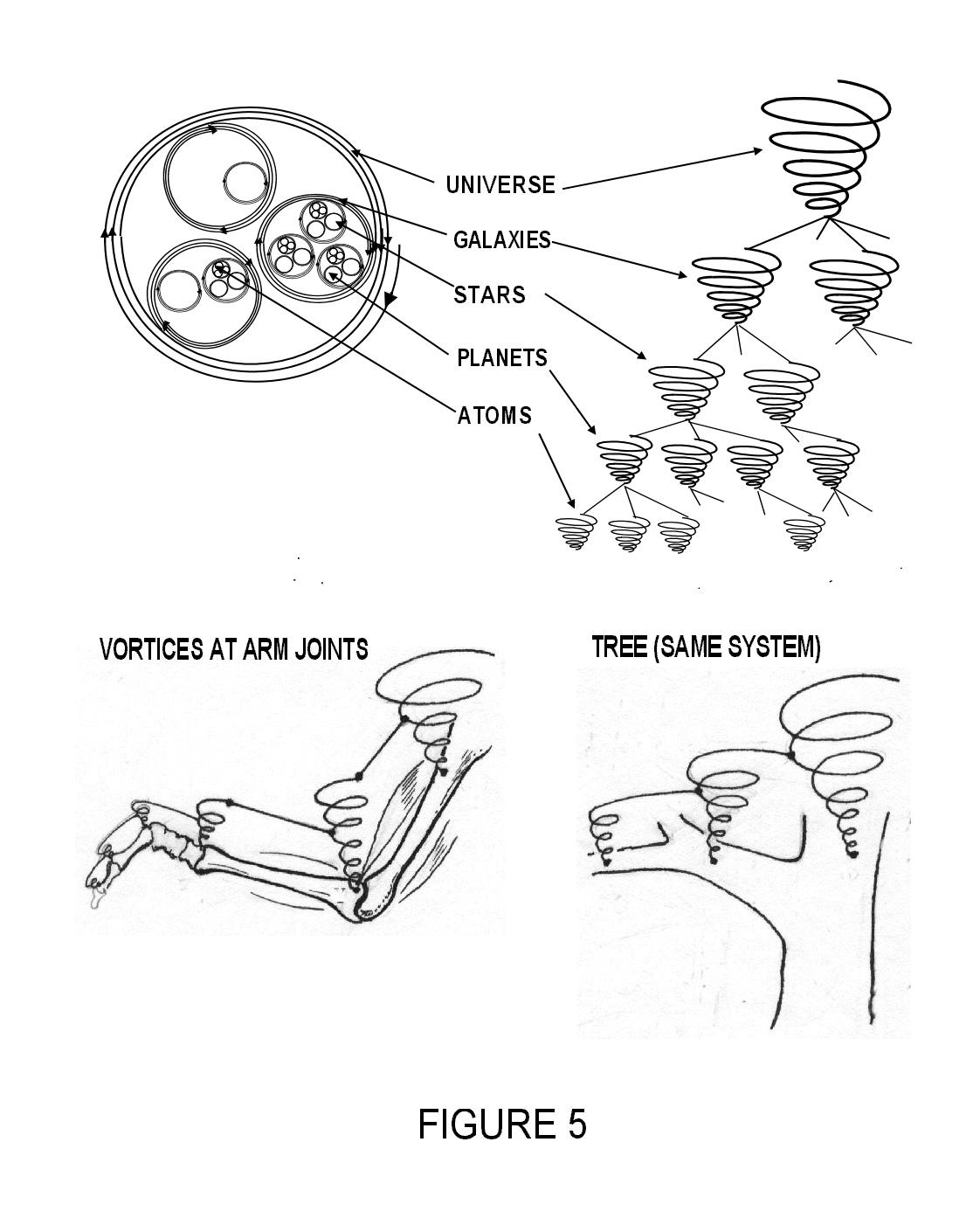
An upper fractal contains the innate programming for ordering
a lower one, such as Earth and an atom, respectively. We shall occasionally
use the analogy of the pyramid company organization, such as the manager being
a higher fractal, giving instructions to a ground-floor worker, a lower fractal.
The ground-floor worker, manager, executive, president, would represent stable
fractals such as in a fern and its fronds, or branches on a tree.
Between and within these fractal levels are the probabilities---the
random area. Prior to the advent of chaos theory (and to some degree quantum
mechanics) scientists thought that the universe was created from a random condition.
This would correspond to the spiral in Figure 1---containing no orders and thus
there would really be no fractals and therefore no existence---there would only
be the particle level. But science tells us the universe is made up of particles
only; however, this is not so. Established fractal levels, such as a planet,
galaxy, etc. are also basic, besides elementary particles.
Randomness and unpredictability are essential though to free
will and creativity. The random areas are the ones with flexibility and instabilities,
available for further programming. The degree of free play between fractals
is proportional to the gap between adjacent global control fractals and local
control fractals. But even this relation is governed by its context and application.
(It is not essential that the following more mathematical analysis is understood.)
If we are applying it to consciousness then it would appear
we are saying that the greater the gap between, say, the soul level and its
human extension, the more free will the human has. But this applies only when
the soul level has set a programme for the human---the soul is free of this
program. If the gap was very small the human would act as one with the soul
more frequently, thus having still greater freedom. Compare the dog's leash
decreasing so that eventually the dog's path is the same as the dog's owner's,
with the freedom that the owner has. (Note: 'human' here, is not to be confused
with the dog's owner in the analogy.)
Thus there are two counter variables when we increase the gap.
If there is a higher programme:
1) the human (soul extension, not the dog analogy)
has more freedom since there are more probabilities available 'around' the programme
(the dog has a longer leash) and the human can, for instance, try some negative,
egotistical paths that are not in the programme,
2) but as we increase the gap,
the effect of the programme becomes more compulsive (enforced) and not within
the choice of the human---it is more unconscious. As we decrease the gap, the
programme is more willingly applied by the human, since it is acting more as
the soul (oneness with the soul).
The fractal levels are programmes of information but will have
boundary conditions that give some free play. For example, a tree might be fixed
to have seven fractal levels:
1) trunk,
2) first large branch,
3) smaller branches
. . . still smaller branches to 7) twigs.
However, the fixed programme does
not say the trunk and the branches must be of exact thicknesses, or that a branch
must begin precisely at such and such a point, or be of such a length before
another offshoot branch forms.
There is thus growth creativity in addition to
growth programming, according to environmental circumstances. For example, the
DNA of a seed or plant will be in continuous communication with higher fractal
collective levels for this species, making selections, within boundary conditions,
for the next cell placement in its growth.
If the programmer is looking for instructions/programming of
the type used in man's artificial computers he won't find them. Man's encoding
systems are relative and arbitrary and essentially are governed by algebra formulae,
which means representations; let this or that equal whatever. Nature's universal
system must be absolute and ubiquitous for all entities and will thus operate
on geometric intelligence.
Another simple analogy is to consider a wire net, which has
square openings between the wires. The wires give the boundary condition, the
dimensional framework for free play and exploration within the squares. However,
we have to imagine many nets of different size openings (fine to coarse) all
superimposed but hierarchically, as are the circles in Figure 1, or as in a
company organization.
The ground-floor worker functions in narrow boundary conditions,
the managers have a wider span of operation and the president would be like
a 'net' with just one big square opening (spanning all the company activities).
Now, in the human body, for example, arm movements, we have
fractals at the fixed points: shoulder, elbow, wrist, fingers. The same basic
model applies here. The shoulder movement contains the larger spiral which is
a vortex (working with the muscles and regulating the angle of the joints),
and the elbow fractal is within this, and so on to the fingers. The fingers
operate in the context of the wrist, the wrist in the context of the elbow,
etc. See article
Free will and Fractals and articles on physical mobility.
This is an efficient system. There could be fractals between shoulder and elbow
or elbow and wrist, that is, more joints. In fact there could be continuous
fractals (joints) along the arm to produce a prehensile arm, as in a monkey's
tail, but the human arm arrangement is considered adequate. We programme the
learning patterns for control of angular movements of fingers, wrist, elbow,
and shoulder.
Psychologists some 30 years ago discovered experimentally that
learning at the shoulder would pass down the ranking system to low levels (fractals)
such as elbow, wrist, fingers (previously explained in detail). But learning
pattern information would not pass up the rank (hierarchical system from fingers
to wrist, elbow, and shoulder). Thus any 'circle' in Figure 1 operates in the
context of any greater circle.
And we are not using an analogy when we say that
the shoulder vortex passes down its information to a smaller elbow joint vortex,
and further to smaller vortices, wrist and fingers, when a sequence of
movements is learned. We are actually stating that storage of information for,
say, a keyboard sequence of movements comes from the shoulder, where the programme
is in a higher-order format and quantum reduces through the lower context and
fractals of elbow and wrist, to the fingers. See articles on physical mobility.
Let us now consider another application of these same fractal
nonlinear programming principles. This particular example will be used intermittently
throughout the text for clarification purposes. Each analogy gives a different
angle on the problem for aiding overall understanding.
Consider a soccer team; though this will be too complex for
a simple example of the way nonlinear programming works. Therefore let us take
the following components only: a goal post, goal keeper, one defense, and one
opponent, or offense/attacker. This example is only an analogy to show the mechanics
of this computer system since, in particular, the players will have free will
(within certain higher-dimensional limits) and be independent of a weak collective
effect---compared with the tree, which has a much more formatted programme.
Since we consider that the energy (of creation or fundamental
programming)---and this is an inherent part of this system---flows from a large
'circle' to a small one, then for illustration purposes we can put in a programme
at level A---see Figure 6. We set the programme at A to give player at D, the
attacker, a goal. Note that this is relevant to anyone setting personal goals.
They might activate the goal postulate at this higher order level (many other
factors must agree though). Nevertheless we are taking an imaginary case here.
Thus the programme has the instruction that a goal is made in, say, a few minutes---because
of the free play between fractal levels this interval is quite flexible.
Let's give the attacker the ball. He basically has countless
probabilities to choose from as an independent entity. But this is now
a programme and all component parts must be interrelated; his probable choices
will be less. The individual mode corresponds to the centre of Figure 1---like
a particle.
 In
Figure 6 we see that A is the 'president' component in the programme which spans
all factors or lower fractal levels. We have in fact already created a fractal
postulate by establishing the goal to be achieved.
In
Figure 6 we see that A is the 'president' component in the programme which spans
all factors or lower fractal levels. We have in fact already created a fractal
postulate by establishing the goal to be achieved.
Figure 6 has been simplified
even beyond our three players and the goal post by reducing the programme to
only four fractal levels A, B, C, D, but in general there would be a gradient
from A to D. This gradient involves the mind and physical processes of the components
of the programme.
Returning to the offensive player with the ball. Although he
has a complete array of probabilities, choices to select from, such as move
right, move left, etc., all these selections will not give the goal because
there is a defense and a goal keeper. Nevertheless D has numerous possibilities
that will lead to the goal which A will emphasize.
Thus we shift now from fractal control at level D to fractal
level C, which spans both defense and attack (keep in mind we are explaining
these, one after the other, D, C, B, A, but they are simultaneous and
that there is really a gradient going back to total control at A).
Level C's
probabilities, which also must lead to the goal, will limit the attack player's
choices still further. But this player will make one of these goal selections
(since levels B and A are operating, giving simultaneous guidance with a necessary
'homing in' gradient to the goal). We see that the available probabilities are
reducing---not in time though; it is simultaneous activity.
Let the offensive player now select a movement, say, to the
right for passing the defense. But all the while this is occurring, in addition
to A, which is influencing the whole scene, fractal programme component B is
functioning and influencing C and D. We may see that B covers the collective
interrelationship between offense, defense, and goal keeper, that is, C and
D.
Beware of thinking in a sequence, but the material level must play off in
time. A learning pattern in skills such as playing a sequence of movements on
a keyboard will span a couple of seconds (or so) by the 'president' level, such
as fractal A, with a gradient breakdown to D; and a sequence in time is achieved
in precisely the same manner as described above. If the reader becomes lost
on this nonlinearity/simultaneous concept, go back to the example of the person
taking a dog, which is on a long leash, for a walk.
The dog can make decisions
where to go within the boundary conditions (context) of the human and leash,
but also the human's decisions, such as where to go, are superimposed on this
for the final outcome or result.
We specially constructed the soccer example so that it would
justify about four fractal levels (which could be understood) but in truth one
should realize that, in general, our programme must handle conceptual as well
as physically-fixed fractal examples, such as in the case of a tree (branches
to twigs), and the full gradient (Figure 1) must be taken into account. Why
is this? Why can't we have subprogrammes at A, B, C, D with gaps between as
illustrated in this simplified example.
This is because continuous (contiguous)
nonlinearity is required, otherwise during those gaps the sequence will have
to be predictable linear paths (because of the enforced programme) with no free
will or interference occurring, such as the players falling down. The gaps would
be acceptable if they could be rigid like the arm arrangement. This is a programme
not designed to have steps in it like the arm and its joints; the programme
must include the viewpoint of the other players and environmental factors.
In the natural condition of this soccer example there would
of course be no head programmer setting a goal to be made, and our example is
essentially fictitious for our level of evolution.. However, note that the players,
with sufficient cohesion of their minds, could quantum regenerate a goal to
be made for their collective group. This means a fractal level at A is now programmed
with the goal result.
It means level A will now superimpose on level D at all
times, influencing what level D produces or selects in the way of probabilities
available to it. Level A would restrict the choices at level D to probabilities
that culminate in the goal. This would be controlled through sub-levels
B and C.
A programme must contain a complete number of fractal steps
according to its requirements and applications. The above fractal strata has
been compared with the arm action: A (shoulder), B (elbow), C (wrist), D (fingers).
But with the arm there is rigidity between the fractal levels (forearm,
upper arm) and programmed fractal levels cannot be added (new joints). Whereas
this is flexible in the soccer example, and as stated must therefore have a
continuous gradient available.
Note that when we refer to 'linear' we mean only one of the
levels would be present, which would be D for us---the material expression---and
then a string of Ds would be a linear programme (as in our computers). Life
and the universe never work this way; they are always nonlinear, as scientists
are beginning to realize.
The reason is that consciousness is inherently multidimensional---a
slice of this 'thickness' would be a limited and 'artificial' viewpoint which
is what we have in this 3D. Let us continue with further analogies and applications
to consciousness in Part II, eventually examining the locomotion aspects of
the energies and physical fractal expressions.
Back to
Contents
 In
2D they are like circles within circles but in 3D or more they are like shells
within shells connected as a total spiral (ideally this should then be envisaged
in 4D to give perfect super-symmetry when we introduce the anti-spiral). This
is the same as the vortex model given in other articles where much more detail
is presented, such as the article,
The Basic Energy Unit ---which, in
particular, shows the higher-dimensional nature of the vortex.
In
2D they are like circles within circles but in 3D or more they are like shells
within shells connected as a total spiral (ideally this should then be envisaged
in 4D to give perfect super-symmetry when we introduce the anti-spiral). This
is the same as the vortex model given in other articles where much more detail
is presented, such as the article,
The Basic Energy Unit ---which, in
particular, shows the higher-dimensional nature of the vortex.

 Figure
4 gives another view of this. The top represents the unity of everything below
it, and corresponds to A. Then B and C are levels further down.
Figure
4 gives another view of this. The top represents the unity of everything below
it, and corresponds to A. Then B and C are levels further down.
 In
Figure 6 we see that A is the 'president' component in the programme which spans
all factors or lower fractal levels. We have in fact already created a fractal
postulate by establishing the goal to be achieved.
In
Figure 6 we see that A is the 'president' component in the programme which spans
all factors or lower fractal levels. We have in fact already created a fractal
postulate by establishing the goal to be achieved.