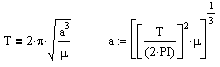by Tom Smith

10/28/02

from QuarkBurger Website
 

In mid-October of 2002, I stumbled across a chat room about Surviving Planet X. This got my interest, so I came in and asked "What's Planet X?". The host pasted a summary and a bunch of links explaining that Planet X orbits every 3600 years, and will swing past the Earth within 14 million miles, causing global devastation.

Immediately I was skeptical, as were others in the room. But I wanted to look at this in an objective, and scientific way. I was close to completing a Masters in Physics, and had recently taken three semesters of orbital mechanics, so I decided to run the numbers.

All objects in space (and on Earth for that matter) follow physical laws. And it turns out the laws of orbital mechanics are actually simpler than many other areas in physics because drag is usually negligible, and planetary bodies, asteroids, stars, etc, do not have the ability to alter their course like a space craft would. By using the laws of gravity to determine motion, the movement of objects in space can be determined far into the future with a high degree of accuracy.

Let's look at Kepler's Laws. They are the foundation of orbital mechanics and are found in the first couple of pages in any orbital mechanics book.

• First Law

  The orbit of each planet is an ellipse, with the sun at a focus.

• Second Law

  The line joining the planet to the sun sweeps out equal areas in equal times.

• Third Law

  The square of the period of a planet is proportional to the cube of its mean distance from the sun.

Since 1609, these laws have held true and have survived basically unchanged for centuries.

(There are two exceptions though:

The first law is now "The orbit of each planet is a conic section (ellipse, parabola or hyperbola), with the sun at a focus".

The additional orbit types are for objects going too fast for the sun to pull it back again. These objects will continue beyond the solar system. The second exception is in extreme cases where velocities approach the speed of light or super massive objects such as black holes are involved. Neither of these exceptions apply here.)

Using these laws, and the equations they translate into, we can actually determine quite a bit using four pieces of information gained from the ZetaTalk website:

1. The period, or time it takes for a complete orbit, is 3657 years.
2. Encounter date of May-June of 2003
3. Planet X's orbit is inclined at 32 degrees from Earth's orbit.
4. Planet X is a brown dwarf

For clarity, here is an orbit diagram which shows the basic properties of an elliptical orbit, and the relationship of Earth's and Planet X's orbit.

Note the elongated shape of the ellipse. This is determined by the eccentricity of the orbit. An eccentricity of 0 is a circle, and the closer it gets to 1.0, the more stretched out it will be. An eccentricity of 1.0 would no longer be an ellipse though, that's a parabola. The eccentricity and the semi-major axis are both important in determining the size and shape of the orbit.

• First we shall determine the semi-major axis, and this comes directly from Kepler's 3rd law.

  

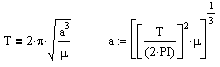
  T is the period (3657 years). From this we can solve for a, the semi-major axis which comes to 237 astronomical units (AU). One AU is the distance from the sun to the Earth.
   

• Second we'll find the eccentricity. From the diagram above, p is the semi-latus rectum. It's a strange name, but basically it is the distance to the point on the ellipse above and below the focus (where the sun is). This is shown on the diagram above as pt1, and pt2. The significance of these points is that with Planet X's orbit inclined, these points are the only points where an encounter with Planet X and Earth can occur.

  

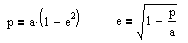
  The left equation computes p, but we already know what p is. Since p is where the encounter occurs, it must be the distance from the sun to the Earth, or 1 AU. So we solve for e (eccentricity), which comes to 0.99789. This would be a highly eccentric orbit. Then the perihelion distance and aphelion distance (closest and furthest point in the orbit) can be determined to be 0.5AU and 474AU respectively.
   

How far is Planet X now?

We can also determine how far away Planet X is based on the number of days until the encounter date. For the purposes of this report, let's use May 31st, 2003 as the encounter date, and for the current time, let's use October 31, 2002. That comes to 212 days. Based on orbital mechanics that are a bit more tricky, (click image below right) one can calculate how far an object will travel in it's orbit over a given period of time. Using this method, I have determined that on 10/31/02, Planet X would have to be 3.35 AU from Earth if it is going to be here by May/June of 2003.

There is no getting around this result. For example if a ball is going to fall from a ledge and hit the ground in 1 second (excluding air drag effects) the ledge must be 32 feet high, since things on Earth fall at 32 feet/second squared. It's just the way it works.

So based on a distance of 3.35AU, and that Planet X is reported to be a brown dwarf (which are typically about 160,000km in diameter), we can also compute the angular diameter of Planet X in our sky, which would be arctan(160,000km/500,000,000km), or 66 seconds of arc. In comparison, Venus is approximately 60 seconds of arc. Planet X should then appear to be slightly larger than Venus, and would be the brightest object in the sky after the sun and moon.

The fact that we can not see Planet X should create serious doubt that it will encounter Earth in May-June of 2003. I predict that the encounter date will come and go without incident, and ZetaTalk will then issue a new date based on some new piece of information they just received. The bottom line is, before you accept something like this as fact, and especially before you go spreading the story, use your head, and check into it.

Click image right for the complete method used to derive these results.

P.S. Update
On 1/1/03 Planet X should be 2.57 AU away, and 85 seconds of arc. This would appear 43% larger than Venus.