A-FIELD IS REAL
SLIDE 6.

|
A – FIELD CAN INFLUENCE THE
MOTION OF ELECTRONS. |
MAGNETIC FIELD AND |
|
|
|
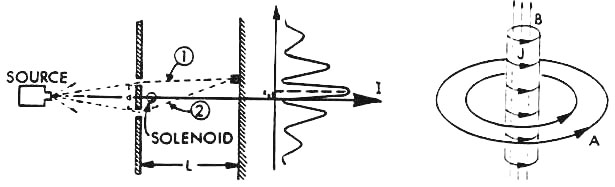
| In classical EM, the vector magnetic
potential (the A-field) had been defined as a mathematical convenience
by the equation
ÑxA = B. [1] But if the potentials are real, then conceivably the A field can be loosed from its enchainment to the Ñx operator. In that case, it becomes a free, new, and independent field of nature with potentially unique characteristics. For example, its defining equation shows that magnetic force field can be made from it, and the rightmost term of the equation E = -ÑØ -dA/dt [2] shows that its time rate of change makes an electric field. Let us explain this in more simple terms, and somewhat more precisely than conventional theory. We will use the Kaluza unified G-EM interpretation and electron flow in our explanation. In the A-field, we have a certain kind of 5-dimensional G-potential which can bleed-off as EM force fields in two ways: (1) in a swirl fashion, where the vortex producing the swirl moves parallel to electron movement, and the swirling is a torque or spin, and (2) in a linear fashion, where the time rate of change of the A-potential produces a linear E-field on the electrons. The first bleed-off as given by equation [1] constitutes the magnetic B-field, and the second bleed-off as given by the rightmost term of equation [2] creates a component of the overall electrical E-field. (Bleed-off of the electrostatic scalar potential produces the other component of the E-field). Now in general relativity (GR) theory, "the" G-potential is just a conglomerate of many things, each of which has the characteristic of curving spacetime. "The" gravitational field is not a single thing at all, but is composed of a collection of many things. Thus if we realize that both the electrostatic scalar potential (Ø-field) and the magnetic vector potential (A-field) are components of the 5-d G-potential, then we see immediately that bleed-off of these two components of the 5-d G-potential creates all normal EM force fields. It follows that, if we produce a zero-vector summation of the two or more EM bleed-offs, we are actually "putting as much back in" to the 5-d G-potential through its A and Ø components as we are taking out electromagnetically. In that case, the 5-potential is in a state of equilibrium with respect to EM bleed-off. It is now forced to bleed-off in the only other way it can: as ordinary 4-dimensional gravitational field. Thus by vector-zeroing EM force fields, we turn EM field energy into G-field energy and vice versa, via the intermediary of the 5-potential. At any rate, soon after publication of the Aharonov-Bohm paper, experiments showed that, if the magnetic field is trapped inside a long solenoid, a phase shift still is induced in the two-slit electron experiment, even though -- classically -- no contact of the enclosed magnetic field and the moving electrons occurs. This phase shift is explained by the fact that the freed A-field exists outside the trapping solenoid, even though the B-field does not. Consequently, interaction of this free A-field with the electrons produces a phase shift of the QM interference detection pattern. This proves that A-field is real and causes physical effects. It also proves that a form of action at a distance is real, just as required by quantum mechanics. Years ago, Frank Golden and this author -- together with Dr. William Tiller -- experimented with "free A-field" devices. Golden went on to develop prototype transmitters and receivers and a prototype underwater communication system. Since that time, Gelinas has patented several curl-free magnetic vector potential (free A-field) devices: see U.S. patent no. 4,447,779, May 8, 1984; 4,429,288, Jan. 31, 1984; 4,429,280, Jan. 31, 1984; and 4,432,098, Feb. 14, 1984. These patents are assigned to Honeywell. (See also Theodor Kaluza, Sitz. Berlin Preuss, Adad. Wiss. 966, 1921.). |