|
|
|
from
Essentia Website
An astonishing theory called the
holographic principle holds that the universe is like a hologram:
just as a trick of light allows a fully three-dimensional image to
be recorded on a flat piece of film, our seemingly three-dimensional
universe could be completely equivalent to alternative quantum
fields and physical laws "painted" on a distant, vast surface.
A ribosome in a cell in your body is supplied with amino acid building blocks and is powered by energy released by the conversion of ATP to ADP, but it can synthesize no proteins without the information brought to it from the DNA in the cell's nucleus.
OUR INNATE PERCEPTION that the world is three-dimensional could be an extraordinary illusion.
Likewise, a century of developments in physics has taught us that information is a crucial player in physical systems and processes.
Indeed, a current trend, initiated by John A. Wheeler
of Princeton University, is to regard the physical world as made of
information, with energy and matter as incidentals.
Remarkably, recent developments in theoretical physics answer some of these questions, and the answers might be important clues to the ultimate theory of reality.
By studying the mysterious properties of black holes, physicists have deduced absolute limits on how much information a region of space or a quantity of matter and energy can hold.
Related results suggest that our universe, which we perceive to have three spatial dimensions, might instead be "written" on a two-dimensional surface, like a hologram. Our everyday perceptions of the world as three-dimensional would then be either a profound illusion or merely one of two alternative ways of viewing reality.
A grain of sand may not encompass our
world, but a flat screen might.
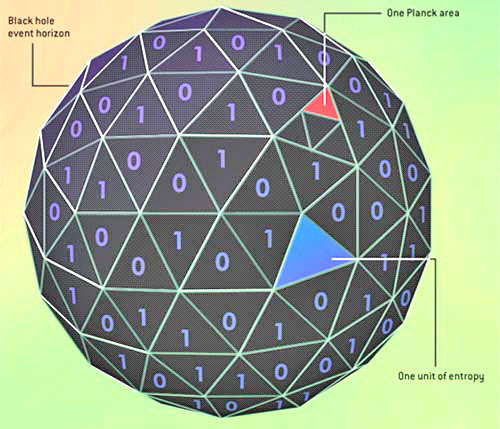
The Entropy of a Black Hole is proportional to the area of its event horizon, the surface within which even light cannot escape the gravity of the hole.
Specifically, a hole with a horizon spanning A Planck areas has A/4 units of entropy. (The Planck area, approximately 10-66 square centimeter, is the fundamental quantum unit of area determined by the strength of gravity, the speed of light and the size of quanta.)
Considered as
information, it is as if the entropy were written on the event
horizon, with each bit (each digital 1 or 0) corresponding to four
Planck areas.
Entropy had long been a central concept of thermodynamics, the branch of physics dealing with heat. Thermodynamic entropy is popularly described as the disorder in a physical system. In 1877 Austrian physicist Ludwig Boltzmann characterized it more precisely in terms of the number of distinct microscopic states that the particles composing a chunk of matter could be in while still looking like the same macroscopic chunk of matter.
For example, for
the air in the room around you, one would count all the ways that
the individual gas molecules could be distributed in the room and
all the ways they could be moving.
The Shannon entropy of a message is the number of binary digits, or bits, needed to encode it. Shannon's entropy does not enlighten us about the value of information, which is highly dependent on context. Yet as an objective measure of quantity of information, it has been enormously useful in science and technology.
For instance, the design of every modern communications device - from cellular phones to modems to compact-disc players - relies on Shannon entropy.
The two entropies have two salient differences, though. First, the thermodynamic entropy used by a chemist or a refrigeration engineer is expressed in units of energy divided by temperature, whereas the Shannon entropy used by a communications engineer is in bits, essentially dimensionless.
That
difference is merely a matter of convention.
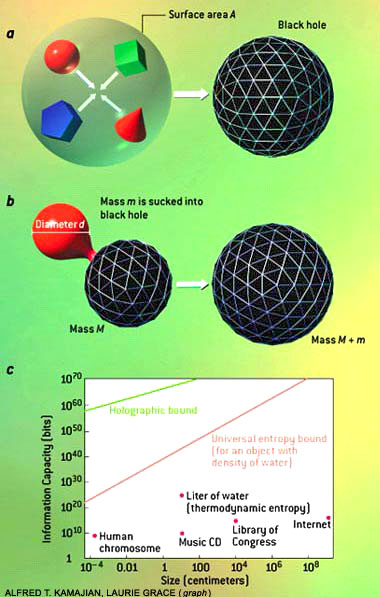
The holographic bound defines how much information can be contained in a specified region of space. It can be derived by considering a roughly spherical distribution of matter that is contained within a surface of area A.
The matter is induced to collapse to form a black hole (a). The black hole's area must be smaller than A, so its entropy must be less than A/4 [see illustration]. Because entropy cannot decrease, one infers that the original distribution of matter also must carry less than A/4 units of entropy or information.
This
result - that the maximum information content of a region of space is
fixed by its area - defies the commonsense expectation that the
capacity of a region should depend on its volume.
The increase in the black hole's size places a limit on how
much entropy the capsule could have contained. This limit is tighter
than the holographic bound, except when the capsule is almost as
dense as a black hole (in which case the two bounds are equivalent).
Even when reduced to common units, however, typical values of the two entropies differ vastly in magnitude.
A silicon microchip carrying a gigabyte of data, for instance, has a Shannon entropy of about 1010 bits (one byte is eight bits), tremendously smaller than the chip's thermodynamic entropy, which is about 1023 bits at room temperature. This discrepancy occurs because the entropies are computed for different degrees of freedom.
A degree of freedom is any quantity
that can vary, such as a coordinate specifying a particle's location
or one component of its velocity.
As miniaturization brings closer the day when
each atom will store one bit of information for us, the useful Shannon entropy of the state-of-the-art microchip will edge closer
in magnitude to its material's thermodynamic entropy. When the two
entropies are calculated for the same degrees of freedom, they are
equal.
toms, after all, are made of electrons and nuclei, nuclei are agglomerations of protons and neutrons, and those in turn are composed of quarks. Many physicists today consider electrons and quarks to be excitations of superstrings, which they hypothesize to be the most fundamental entities. But the vicissitudes of a century of revelations in physics warn us not to be dogmatic.
There could be more levels of
structure in our universe than are dreamt of in today's physics.
(This ambiguity causes no problems in analyzing practical thermodynamics, such as that of car engines, for example, because the quarks within the atoms can be ignored - they do not change their states under the relatively benign conditions in the engine.)
Given the dizzying
progress in miniaturization, one can playfully contemplate a day
when quarks will serve to store information, one bit apiece perhaps.
How much information would then fit into our one-centimeter cube?
And how much if we harness superstrings or even deeper, yet undreamt
of levels? Surprisingly, developments in gravitation physics in the
past three decades have supplied some clear answers to what seem to
be elusive questions.
That simple rule must break down for a large enough
pile of chips because eventually the information would exceed the
holographic bound, which depends on the surface area, not the
volume. The "breakdown" occurs when the immense pile of chips
collapses to form a black hole. Black Hole Thermodynamics
Black holes are a consequence of general relativity, Albert Einstein's 1915 geometric theory of gravitation. In this theory, gravitation arises from the curvature of spacetime, which makes objects move as if they were pulled by a force.
Conversely, the curvature is caused by the presence of matter and energy. According to Einstein's equations, a sufficiently dense concentration of matter or energy will curve spacetime so extremely that it rends, forming a black hole. The laws of relativity forbid anything that went into a black hole from coming out again, at least within the classical (nonquantum) description of the physics.
The point of no return, called the event
horizon of the black hole, is of crucial importance. In the simplest
case, the horizon is a sphere, whose surface area is larger for more
massive black holes.
If the matter is captured while circling the hole, its associated angular momentum is added to the black hole's angular momentum. Both the mass and angular momentum of a black hole are measurable from their effects on spacetime around the hole. In this way, the laws of conservation of energy and angular momentum are upheld by black holes.
Another fundamental law, the second law of thermodynamics,
appears to be violated.
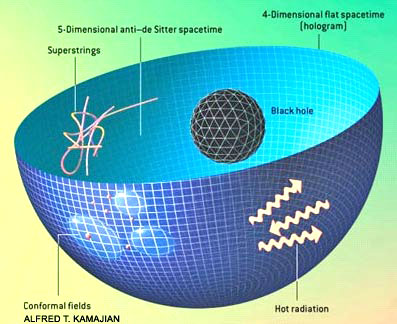
Theorists have demonstrated this principle mathematically for a specific type of five-dimensional spacetime ("antide Sitter") and its four-dimensional boundary. In effect, the 5-D universe is recorded like a hologram on the 4-D surface at its periphery. Superstring theory rules in the 5-D spacetime, but a so-called conformal field theory of point particles operates on the 4-D hologram.
A black hole in the 5-D spacetime is equivalent to hot radiation on the hologram - for example, the hole and the radiation have the same entropy even though the physical origin of the entropy is completely different for each case.
Although these two descriptions of the universe seem utterly unalike, no experiment could distinguish between them, even in principle.
The second law of thermodynamics summarizes the familiar observation that most processes in nature are irreversible: a teacup falls from the table and shatters, but no one has ever seen shards jump up of their own accord and assemble into a teacup.
The second law of thermodynamics
forbids such inverse processes. It states that the entropy of an
isolated physical system can never decrease; at best, entropy
remains constant, and usually it increases. This law is central to
physical chemistry and engineering; it is arguably the physical law
with the greatest impact outside physics.
A clue to resolving this puzzle came in 1970, when Demetrious Christodoulou, then a graduate student of Wheeler's at Princeton, and Stephen W. Hawking of the University of Cambridge independently proved that in various processes, such as black hole mergers, the total area of the event horizons never decreases.
The analogy with the tendency of entropy to increase led me to propose in 1972 that a black hole has entropy proportional to the area of its horizon.
I conjectured that when matter falls into a black hole, the increase in black hole entropy always compensates or overcompensates for the "lost" entropy of the matter. More generally, the sum of black hole entropies and the ordinary entropy outside the black holes cannot decrease.
This is
the generalized second law - GSL for short.
Even in thermodynamic terms, this is a vast quantity of entropy.
The entropy
of a black hole one centimeter in diameter would be about 1066 bits,
roughly equal to the thermodynamic entropy of a cube of water 10
billion kilometers on a side.
In 1980 I began studying the first such bound, called the universal entropy bound, which limits how much entropy can be carried by a specified mass of a specified size [see box on opposite page].
A related idea, the
holographic bound, was devised in 1995 by Leonard Susskind of
Stanford University. It limits how much entropy can be contained in
matter and energy occupying a specified volume of space.
The black hole entropy is therefore smaller than A/4. According to the GSL, the entropy of the system cannot decrease, so the mass's original entropy cannot have been bigger than A/4. It follows that the entropy of an isolated physical system with boundary area A is necessarily less than A/4.
What if the mass does not spontaneously collapse?
In 2000 I showed that a tiny black
hole can be used to convert the system to a black hole not much
different from the one in Susskind's argument. The bound is
therefore independent of the constitution of the system or of the
nature of level X. It just depends on the GSL.
Estimating the entropy of the universe is a
difficult problem, however, and much larger numbers, requiring a
sphere almost as big as the universe itself, are entirely plausible.
depends on the boundary area instead of the volume. Imagine that we are piling up computer memory chips in a big heap. The number of transistors - the total data storage capacity - increases with the volume of the heap.
So, too, does the total thermodynamic entropy of all the chips.
Remarkably, though, the theoretical ultimate information capacity of the space occupied by the heap increases only with the surface area.
Because volume increases more rapidly than surface area, at some point the entropy of all the chips would exceed the holographic bound. It would seem that either the GSL or our commonsense ideas of entropy and information capacity must fail.
In fact, what fails is the pile itself: it would collapse under its own gravity and form a black hole before that impasse was reached.
Thereafter each additional memory chip would increase the mass and
surface area of the black hole in a way that would continue to
preserve the GSL.
In the everyday world, a hologram is a special kind of photograph that generates a full three-dimensional image when it is illuminated in the right manner. All the information describing the 3-D scene is encoded into the pattern of light and dark areas on the two-dimensional piece of film, ready to be regenerated.
The holographic principle contends that an analogue of this visual magic applies to the full physical description of any system occupying a 3-D region: it proposes that another physical theory defined only on the 2-D boundary of the region completely describes the 3-D physics.
If a 3-D system can be
fully described by a physical theory operating solely on its 2-D
boundary, one would expect the information content of the system not
to exceed that of the description on the boundary.
The real universe is a 4-D system: it has volume and extends in time. If the physics of our universe is holographic, there would be an alternative set of physical laws, operating on a 3-D boundary of spacetime somewhere, that would be equivalent to our known 4-D physics.
We do not yet know of any such 3-D theory that works in
that way. Indeed, what surface should we use as the boundary of the
universe? One step toward realizing these ideas is to study models
that are simpler than our real universe.
De Sitter's spacetime is empty, expands at an accelerating rate and is very highly symmetrical.
In 1997 astronomers studying distant supernova explosions concluded that our universe now expands in an accelerated fashion and will probably become increasingly like a de Sitter spacetime in the future. Now, if the repulsion in Einstein's equations is changed to attraction, de Sitter's solution turns into the anti-de Sitter spacetime, which has equally as much symmetry.
More important for the holographic concept, it possesses a boundary,
which is located "at infinity" and is a lot like our everyday spacetime.
Juan Maldacena, then at Harvard University, first conjectured such a relation in 1997 for the 5-D anti-de Sitter case, and it was later confirmed for many situations by Edward Witten of the Institute for Advanced Study in Princeton, N.J., and Steven S. Gubser, Igor R. Klebanov and Alexander M. Polyakov of Princeton University.
Examples of this holographic
correspondence are now known for spacetimes with a variety of
dimensions.
(Of course, the structures of their brains might give
them an overwhelming "commonsense" prejudice in favor of one
description or another, in just the way that our brains construct an
innate perception that our universe has three spatial dimensions;
see the illustration on the opposite page.)
The correspondence works the other way, too. Witten has shown that a black hole in anti-de Sitter spacetime corresponds to hot radiation in the alternative physics operating on the bounding spacetime.
The entropy of the
hole - a deeply mysterious concept - equals the radiation's entropy,
which is quite mundane.
Even if we approximate
our real universe with one that has matter and radiation spread
uniformly throughout, we get not an anti-de Sitter universe but
rather a "Friedmann-Robertson-Walker" universe. Most cosmologists
today concur that our universe resembles an FRW universe, one that
is infinite, has no boundary and will go on expanding ad infinitum.
Susskind's argument based on collapse to a black
hole is of no help here. Indeed, the holographic bound deduced from
black holes must break down in a uniform expanding universe. The
entropy of a region uniformly filled with matter and radiation is
truly proportional to its volume. A sufficiently large region will
therefore violate the holographic bound.
One then imagines a brief burst of light issuing simultaneously and perpendicularly from all over one side of the surface. The only demand is that the imaginary light rays are converging to start with.
Light emitted from the inner surface of a spherical shell, for instance, satisfies that requirement.
One then considers the entropy of the matter and radiation that these imaginary rays traverse, up to the points where they start crossing. Bousso conjectured that this entropy cannot exceed the entropy represented by the initial surface - one quarter of its area, measured in Planck areas.
This is a different way of tallying up the entropy than that used in the original holographic bound.
Bousso's bound refers not to the entropy
of a region at one time but rather to the sum of entropies of
locales at a variety of times: those that are "illuminated" by the
light burst from the surface.
When these conditions are
overstepped - as for a collapsing sphere of matter already inside a
black hole - these bounds eventually fail, whereas Bousso's bound
continues to hold. Bousso has also shown that his strategy can be
used to locate the 2-D surfaces on which holograms of the world can
be set up.
The proliferation of variations on the holographic motif makes it clear that the subject has not yet reached the status of physical law. But although the holographic way of thinking is not yet fully understood, it seems to be here to stay. And with it comes a realization that the fundamental belief, prevalent for 50 years, that field theory is the ultimate language of physics must give way.
Fields, such as the electromagnetic field, vary continuously from point to point, and they thereby describe an infinity of degrees of freedom. Superstring theory also embraces an infinite number of degrees of freedom. Holography restricts the number of degrees of freedom that can be present inside a bounding surface to a finite number; field theory with its infinity cannot be the final story.
Furthermore, even if the infinity is tamed, the mysterious
dependence of information on surface area must be somehow
accommodated.
The chain of reasoning involving holography suggests to some, notably Lee Smolin of the Perimeter Institute for Theoretical Physics in Waterloo, that such a final theory must be concerned not with fields, not even with spacetime, but rather with information exchange among physical processes.
If so, the vision of
information as the stuff the world is made of will have found a
worthy embodiment.
|